4. Základy analýzy elektrických obvodů
| Metoda obvodových proudů | Metoda uzlových napětí | Další metody vhodné k analýze sítí |
Přímá aplikace Kirchhoffových zákonů je u složitějších sítí nadmíru komplikovaná a vede na řešení soustavy neúnosně mnoha lineárních rovnic přičemž není zajištěno, že soustava bude řešitelná (rovnice mohou být lineárně závislé). Z tohoto důvodu se k řešení používají dvě metody, které množství rovnic výrazně redukují. Jsou založeny na takové volbě proudů, resp. napětí, která a priori splňuje první, resp. druhý Kirchhoffův zákon. Rovnice pak píšeme na základě "zbylého" zákona, tedy jen jednoho, a proto je počet rovnic výrazně redukován.
| 4.1. Metoda obvodových proudů |
V této metodě nevyznačujeme proudy v jednotlivých větvích, ale proudy tzv. obvodové (smyčkové), které jsou konstantní podél vybrané uzavřené smyčky. Tím, že proudy vedou podél uzavřené smyčky, musejí každým uzlem sítě jen procházet, tj. vtékat i vytékat. Proudy v jednotlivých větvích sítě jsou pak dány jednoduchým součtem nebo rozdílem (podle orientace) těch obvodových proudů, které jsou dané větvi společné. První Kirchhoffův zákon je tedy pro takto zvolené obvodové proudy splněn automaticky. Jediným problémem v metodě obvodových proudů je nalezení "správného" počtu tzv. nezávislých smyček, pro které píšeme rovnice druhého Kirchhoffova zákona. Pro určení tohoto počtu existují 3 metody:
- grafická metoda; schema obvodu překreslíme do roviny tak, aby nedocházelo ke křížení spojovacích vodičů bez vodivého spojení (tj. vodiče se mohou křížit jenom v uzlu). Pak počet nezávislých smyček je dán počtem "okének" v rovině nákresu, která jsou ohraničena větvemi sítě. Tato metoda je nejjednodušší a ve své praxi s ní plně vystačíte.
- metoda úplného stromu; vztvoříme tzv. úplný strom, tj. podmnožinu sítě s následujícími vlastnostmi: (a) všechny uzly původní sítě jsou propojeny větvemi úplného stromu, (b) vlastnost (a) se ztrácí po vyjmutí libovolné větve úplného stromu. Počet větví, které musíme k úplnému stromu dodat, abychom dostali původní síť je pak roven počtu nezávislých smyček.
- metoda výpočtu; vychází z topologických vlastností sítí. Základem této metody je vztah, který spojuje počet prvků sítě, V, počet tzv. nezávislých uzlů, U, a počet nezávislých smyček sítě, S. Počet nezávislých uzlů sítě dostaneme z celkového počtu uzlů sítě odečetením počtu částí sítě, které jsou od sebe galvanicky odděleny (je-li celá síť galvanicky propojena, odečítáme jedničku, obsahuje-li síť např. jeden transformátor, který galvanicky odděluje obvod primáru od obvodu sekundáru, odečítáme dvojku apod.; pro každou galvanicky oddělenou část sítě odečítáme další jedničku). Platí totiž zcela obecně, že V=U+S.
Určení počtu nezávislých smyček je pro metodu obvodových proudů zcela základní, neboť v případě přeurčení tohoto počtu budou rovnice lineárně závislé, v případě podurčení můžeme dostat chybný výsledek; snadno totiž můžeme "šikovnou" volbou menšího počtu složitěji vedených smyček (volba smyček je zcela libovolná, tj. výše uvedenými metodami zjistíme pouze jejich počet, nikoliv jejich "polohu" v síti) "projít" všechny větve sítě, což může vést k mylnému přesvědčení, že obvod je již určen. Metoda obvodových proudů nemá v tomto smyslu korektiv; spočteme prostě systém méně rovnic o méně neznámých, ale výsledek bude špatně, podurčíme-li počet nezávislých smyček. Při psaní vlastních rovnic mohu jen doporučit důsledné dodržování znaménkových konvencí, tj. předem si označit směry proudů (libovolně) a šipky u zdrojů a pak teprve psát rovnice. Jen tak se vyhnete znaménkovým chybám, které mohou vést k nesmyslným výsledkům. A ještě jedna poznámka: prochází-li smyčkový proud zdrojem proudu, je přímo roven tomuto proudu. Máme-li tedy obvod, kde se zdroj proudu vyskytuje, je vhodné jeden ze smyčkových proudů (a jenom jeden) vést tímto zdrojem. Zredukujeme tak počet potřebných rovnic.
| 4.2. Metoda uzlových napětí |
Označíme si napětí na jednotlivých uzlech sítě tak, že všechna napětí vztahneme k napětí na jednom referenčním uzlu, jehož potenciál položíme definitoricky rovný nule. Máme-li síť, která obsahuje několik galvanicky oddělených obvodů (transformátorem, optickým vazebním členem apod.), musíme si vytyčit referenční uzel v každé galvanicky oddělené části sítě. Takto stanovená uzlová napětí automaticky splňují druhý Kirchhoffův zákon a proto pro úplné určení sítě stačí napsat pro každý uzel (kromě referenčních) Kirchhoffův zákon o proudech v uzlu. Je-li některý z uzlů připojen k referenčnímu uzlu zdrojem napětí, je napětí uzlu známé a můžeme napsat o jednu rovnici méně (duální obdoba smyčkového proudu procházejícího zdrojem proudu). Určení počtu nezávislých uzlů je velmi jednoduché (viz výše v diskusi o určování počtu nezávislých smyček) a tak se napsání rovnic obejde bez větších problémů. Musíme si ale uvědomit, že řešením rovnic dostaneme uzlová napětí a z nich teprve musíme určit proudy v jednotlivých větvích jako napětí na větvi děleno odporem větve; to však je již jen mechanická práce.
Rozhodnout předem, která metoda je výhodnější, není možné, neboť volba metody je závislá na konkrétní síti, kterou studujeme. Pokud má síť méně uzlů, které jsou propojeny více větvemi, je výhodnější metoda uzlových napětí, ale pro jednoduché příklady, které budeme v tomto textu řešit, budeme používat metodu obvodových proudů. Doporučuji ale, abyste si vyřešili některé příklady sítí oběma metodami, neboť jedině tak získáte cit pro to, kolik úsilí která metoda vyžaduje a hlavně se přesvědčíte, že obě metody vedou k cíli.
| 4.3. Další metody vhodné k analýze sítí |
Uvedeme si nyní několik pomocných metod, která mohou vést ke zjednodušení studované sítě a tím k rychlejší cestě k cíli.
- záměna hvězda-trojúhelník
Někdy se při řešení sítí setkáme s odporovým trojpólem tvaru hvězdy nebo trojúhelníka, viz. obr. 1.16a 1.16b.
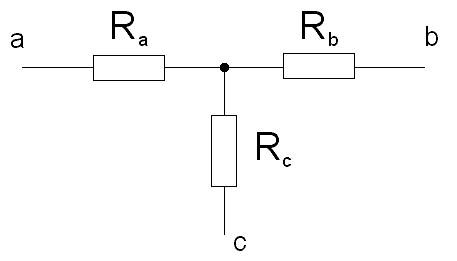
obr 1.16a
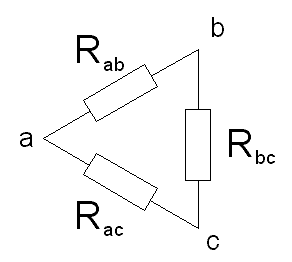
obr 1.16b
Tyto trojpóly jsou navzájem záměnné a mnohdy tím můžeme docílit zjednodušení sítě. Označíme si vrcholy trojúhelníka a odpovídající vrcholy hvězdy písmeny a, b, c. Odpory jednotlivých ramen hvězdy označíme Ra, Rb, Rc podle příslušnosti ramene k vrcholu. Obdobně označíme odpory ramen trojúhelníka Rab, Rbc, Rac. Počítejme odpory mezi vrcholy a, b hvězdy. Tento odpor je roven Ra + Rb. U trojúhelníka je tento odpor roven paralelní kombinaci odporu Rab s odporem daným součtem Rac + Rbc. Vzhledem k tomu, že chceme nahradit hvězdu trojúhelníkem, případně trojúhelník hvězdou, musí se odpor mezi vrcholy a, b u hvězdy rovnat odporu mezi vrcholy a, b u trojúhelníka, čímž dostáváme první rovnici. Obdobně pro vrcholy b, c a c, a dostaneme další dvě rovnice, které můžeme řešit buď pro neznámé Ra, Rb, Rc nebo pro neznámé Rab, Rac, Rbc. Dostaneme tyto vztahy:
Rab = (RaRb + RbRc + RcRa)/Rc
a analogické dva, které se dají popsat následovně:Odpor strany trojúhelníka je roven součtu 3 možných součinů odporů větví hvězdy dělenému odporem protilehlé strany hvězdy. Pro hvězdu dostaneme:
Ra = RabRca/(Rab + Rbc + Rca);
slovy: odpor větve hvězdy je roven součinu odporů asociovaných větví trojúhelníka (větví, které mají společný stejný vrchol) dělenému součtem odporů všech tří stran trojúhelníka. V anglické literatuře se tato transformace nazývá delta-Y substitution, je možno hovořit také o záměně T a p článku (užívá se v teorii filtrů).
- věta o reciprocitě
Mějme lineární síť, ve které je jenom jeden zdroj napětí, ostatní prvky jsou pasivní; předpokládejme, že zdroj je zapojen v k-té větvi. Studujme nyní proud v l-té větvi sítě. Věta o reciprocitě nám říká, že stejný proud, jaký vyvolá zdroj v l-té větvi, vyvolá tentýž zdroj v k-té větvi, zapojíme-li ho do l-té větve (a svorky zdroje v k-té větvi spojíme nakrátko). Tato věta se moc často nehodí, je ale velice elegantní a předpokládá se, že člověk s fyzikálním vysokoškolským vzděláním by ji měl znát.
- propojovací pravidlo
Mějme symetrickou síť, z jejíhož schematu je na první pohled evidentní, že v ní existuje alespoň jedna dvojice uzlů, které jsou na stejném potenciálu. Pak se poměry v síti nezmění, propojíme-li tyto dva uzly zkratem. Toto pravidlo občas pomáhá řešit symetrické obvody jako "určete odpor mezi vrcholy ležící na stěnové (tělesové) úhlopříčce krychle jejíž hrany jsou tvořeny rezistory o odporech r."
- věta o přizpůsobení
Maximální výkon, který je zdroj o vntřním odporu Ri schopen dodat do zátěže s odporem R, nastává pro R=Ri. V případě, že obě veličiny jsou komplexní, nastává maximální výkon (optimální přizpůsobení) tehdy, jsou-li reálné složky sobě rovné a imaginární složky mají opačné znaménko.
Zrekapitulovali jsme si základní pojmy z teorie lineárních sítí. Pojmy, které jsme zavedli, i některé ze zmíněných metod budeme používat v dalším výkladu. Doporučuji, abyste si své praktické dovednosti v řešení problémů z elektrických obvodů sami z vlastní iniciativy prověřili, sbírek úloh je velmi mnoho, na MFF napsaná výborná sbírka úloh z obvodů je v rámci skript "Sbírka úloh z elektřiny a magnetismu", autoři D. Slavínská a kolektiv. Pro vaši školní praxi bude i vhodné, budete-li si shromažďovat příklady z fyziky k přijímacím zkouškám na MFF, ty lze dostat na studijním oddělení a vždy je v nich několik zajímavých úloh z elektřiny, ev. z obvodů. Pro zajímavost: jaký je vnitřní odpor děliče napětí složeného z odporů R1 a R2, je-li připojen na zdroj napětí E (výstup děliče je na odporu R2)?