3.1.2. Elektronová a děrová vodivost pevných látek

V tomto odstavci budeme předpokládat, že ve vodivostním pásu polovodiče, eventuelně v překrývajících se pásech kovu je dostatečná koncentrace volných elektronů a budeme studovat, co se s nimi děje není-li na látku přiložené elektrické pole a dále s přiloženým elektrickým polem. Nejprve první případ. Spočítáme-li nejpravděpodobnější rychlost elektronu z Maxwellovského rozdělení energií pro pokojovou teplotu (zde si, jak již víme, můžeme dovolit nahradit přesný popis daný Fermi-Diracovským rozdělením, Maxwell-Boltzmannovským rozdělením) podle známého vztahu v_p= (8 kT/pm)^1/2, dostaneme hodnotu v řádu 10⁵ m/s. Jak to, že látkou neteče elektrický proud, když je rychlost elektronů tak vysoká? Odpověď dává studium pohybu elektronu v látce. Spočítanou rychlostí se elektron nepohybuje dlouhou dobu, neboť za střední volnou dráhu cca 10^-8 m interaguje s ”různými objekty” v krystalické mříži, jako jsou atomy, fotony, fonony a ostatní elektrony. To má za následek, že směr jeho dráhy se změní. Elektron se tedy pohybuje zcela náhodnými směry, viz obr.3.8.

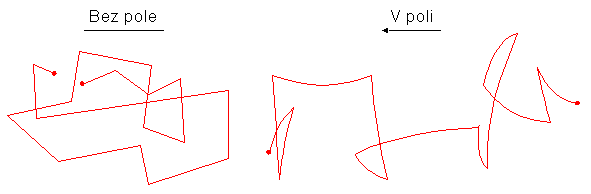
obr. 3.8

Díváme-li se na celkový střední elektrický proud proteklý určitým makroskopickým průřezem vodiče za ”rozumně dlouhou” dobu, je nutně tento střední proud roven nule. Když však připojíme vodič k citlivému přístroji, na kterém máme možnost sledovat i rychlé změny napětí (osciloskop), uvidíme, že na koncích vodiče existuje malé střídavé napětí, jehož efektivní hodnota roste úměrně s teplotou, odporem vodiče a šířkou frekvenčního pásma přístroje D f, kterým toto napětí sledujeme, u_ef²=4k.T.R.D f. (Zde k je Boltzmannova konstanta.) Toto napětí, způsobené právě tepelným pohybem elektronů nazýváme thermální, nebo Nyquistův šum a pro naše úvahy není zatím podstatné.

Umístíme-li látku do elektrického pole, elektron zachovává svůj tepelný pohyb, ale jeho střední rychlost již není rovna nule, ale směřuje ve směru přiloženého elektrického pole. Této střední rychlosti se říká driftová rychlost a fyzikálnímu efektu drift elektronů v elektrickém poli. Driftová rychlost elektronů je definována vztahem

v_dn=m_n.E,

kde veličině m_n říkáme pohyblivost elektronů. Pokud je driftová rychlost malá ve srovnání s tepelnou rychlostí, je úměrná přiloženému poli E a platí Ohmův zákon v diferenciálním tvaru

i=s_n.E,

kde i je proudová hustota (proud na jednotku plochy průřezu vodiče) a m_n je tzv. (elektronová) vodivost látky (nebudeme stále opakovat, že se jedná o elektrickou vodivost, tepelnou vodivostí se v tomto učebním textu nebudeme zabývat). Je-li v látce koncentrace volných elektronů n a ty se pohybují driftovou rychlostí v_dn, projde za jednotkou času jednotkou plochy průřezu vodiče náboj

e.n.v_dn=e.n.m_n.E,

z čehož plyne pro vodivost

s_n=e.n.m_n

(e je náboj elektronu). Zde vidíme odpověď na otázku položenou v konci předchozího odstavce. Díky různé krystalové struktuře vodiče se liší pohyblivost elektronů ve vodiči a tím se liší i vodivost různých vodivých materiálů. Vidíme, že v kovech je vodivost dána výhradně pohybem elektronů jako nosičů nábojen a proto tuto vodivost nazýváme elektronovou vodivostí.

Vodivost izolantů je zanedbatelně malá a proto má smysl probrat nyní jak to vypadá s vodivostí materiálů, u kterých existuje zakázaný pás mezi valenčním a vodivostním pásem, ale jeho šířka není příliš veliká. Znamená to, že vlivem termické excitace existuje určitá koncentrace elektronů ve vodivostním pásu látky a tyto elektrony přispívají k vedení proudu stejným způsobem jak bylo právě popsáno u vodičů. Na rozdíl od vodičů musíme nyní analyzovat ještě situaci ve valenčním pásu. Při teplotě absolutní nuly je tento pás plně obsazen a nejsou zde tedy volné energetické hladiny. Při teplotě vyšší než absolutní nula jsou některé elektrony excitovány do vodivostního pásu. Je zřejmé, že to budou elektrony obsazující energetické hladiny nejblíže horní hranici valenčního pásu, tj. ty nejvyšší energetické hladiny, neboť pravděpodobnost, že budou excitovány elektrony obsazující nižší energetické hladiny ubývá exponenciálně se ”vzdáleností” (tj. energetickou odlehlostí) příslušné hladiny od horní hranice valenčního pásu. Ve valenčním pásu jsou tedy při, pro jednoduchost pokojové, teplotě volné nejvýše položené energetické hladiny a je jich tam stejné množství (stejná koncentrace), jako elektronů ve vodivostním pásu. Při umístění látky do elektrického pole dojde k postupnému obsazování těchto hladin elektrony, které jsou polem urychlovány, aniž ovšem tyto elektrony byly excitovány do vodivostního pásu. To má za následek, kvalitativně řečeno, efektivní pohyb volných energetických hladin ve směru opačném, než je směr elektrického pole. V látce, kde existuje zakázaný pás o nenulové šířce, existuje rovněž ještě další mechanismus přenosu náboje, a sice ve valenčním pásu. Je úmluvou stanoveno (a vychází to také z kvantově-mechanického modelu), že tento mechanismus se popisuje pohybem nosičů s nábojem opačné polarity, tzv. děr (angl. holes). U látky, kde existuje zakázaný pás o nenulové šířce, je tedy celková vodivost daná součtem dvou příspěvků, elektronové vodivosti způsobené pohybem elektronů ve vodivostním pásu, a děrové vodivosti způsobené pohybem děr ve valenčním pásu,

s = s_n+ s_p.

Děrová vodivost s_p je dána obdobným vztahem jako elektronová vodivost, tj.

s_p= e.p.m_p,

kde p je koncentrace děr ve valenčním pásu, v doposud diskutovaném případě rovná koncentraci elektronů ve vodivostním pásu, p = n. Jak uvidíme za chvíli, tento vztah přestává platit, je-li do čistého, tzv. vlastního (intrinsického) polovodiče přimíchána určitá příměs. Dá se ukázat, že pro koncentraci děr ve valenčním pásu platí obdobný vztah jako pro koncentraci elektronů ve vodivostním pásu a sice

p=(1/4)(8pm_p*.k.T/h²)^3/2.T^3/2exp(-(E_F-E_v)/kT),

kde E_v je hodnota energie odpovídající horní hranici valenčního pásu, m_p* tzv. efektivní hmotnost díry. Je zvykem označovat veličinu n = p = n_i jako tzv. vlastní (intrinsickou) koncentraci nosičů náboje. Porovnáme-li vztahy pro n a p vidíme, že součin

n_i²=n.p=2.((m_e*m_p*).p.kT/h²)³exp(-E_g/kT)

nezávisí na poloze Fermiho hladiny, ale jenom na šířce zakázaného pásu. Dá se ukázat, že tento součin nezávisí ani na koncentraci příměsí a že je to tedy veličina charakterizující materiál a závisící jen na teplotě. Pro zajímavost můžeme s použitím vztahů pro n a p vypočítat polohu Fermiho meze ve vlastním polovodiči; ze vztahu n = p plyne

m_e*^3/2exp(-(E_c-E_F)/kT)=m_p*^3/2exp(-(E_F-E_v)/kT).

Logaritmováním a řešením pro E_F dostáváme

E_F=(1/2)(E_v+E_c)+(3/4)kTln(m_e*/m_p*).

Pro teplotu absolutní nuly leží, jak bylo výše uvedeno Fermiho hladina přesně uprostřed zakázaného pásu, pro vyšší teploty je obecně na teplotě závislá, neboť obecně m_e* je různé od m_p*.

Příměsové polovodiče