3.1.4. PN přechod

Předpokládejme, že se nám podařilo nějakým způsobem vytvořit přechod PN, tj. rozdělit vzorek křemíku myšlenou rovinou. V jedné polorovině materiál dotujeme příměsemi typu n a ve druhé příměsemi typu p. V předchozím odstavci již bylo popsáno, že reálná technologie výroby přechodu PN je založena na faktu, že polovodič jednoho typu vodivosti lze ”předopovat” na opačný typ vodivosti. Skutečný PN přechod se tedy vyrábí tak, že se polovodič jednoho typu vodivosti obohatí v určitém objemu příměsemi opačného typu vodivosti; rozhraní tohoto objemu a původního objemu pak tvoří PN přechod. Obohacení příměsemi se děje nejčastěji buď termickou difuzí, kdy do polovodiče ohřátého na vysokou teplotu difundují skrze povrch polovodiče příměsi z atmosféry, která polovodič obklopuje, nebo tzv. iontovou implantací. Při iontové implantaci se atomy příměsí v plynném stavu ionizují, urychlují a fokusují do svazku s průměrem menším než mikron. Svazek dopadá na povrch polovodiče a proniká do hloubky, určené energií iontů. Při průchodu iontu materiálem dochází k jeho zachycení na určité pozici v krystalové mřížce a zároveň k jeho neutralizaci. Výhoda termické difuze je v relativně jednoduché technologii, výhoda iontové implantace ve velmi přesném vymezení obohacené oblasti.

Pro jednoduchost zkoumejme nyní jednorozměrný model. V tomto modelu předpokládáme tzv. náhlý přechod (abrupt junction), tj. do určité souřadnice x_o je materiál typu p a od téhož x_o je materiál typu n. Na obrázku 3.12 je tato situace zachycena pro x_o=0.

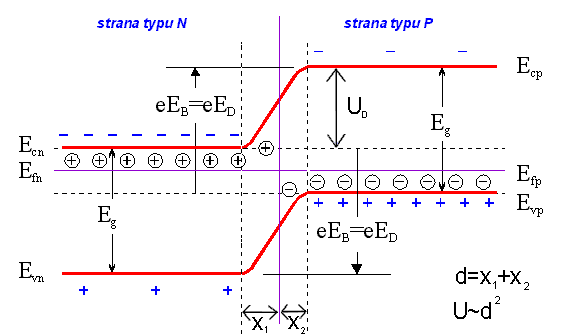
obr. 3.12

Na ose úseček je tedy vynesen jeden rozměr našeho modelu, na ose pořadnic je vynesena energie. Z definice Fermiho energie plyne, že pokud je krystal materiálu v rovnováze, existuje jen jedna hodnota energie, nad kterou jsou při teplotě absolutní nuly všechny energetické hladiny prázdné a pod kterou za stejné podmínky plně obsazené. V našem modelu bude tedy hodnota E_F nezávislá na x, pokud bude krystal v rovnováze. Když ale přiložíme vnější napětí nebo přechod ozáříme fotony o vhodné vlnové délce, porušíme rovnováhu a výslekem pak bude schodovitá změna Fermiho hladiny pro x=0. Zabývejme se však nejprve rovnovážným případem a diskutujme, co se stane, když přechod PN vytvoříme. Vysvětleme si nejprve poněkud přesněji pojem difuze. Ze základní přednášky Molekulová fyzika, z vlastní zkušenosti i ze středoškolských znalostí víme, že v plynu nastává usměrněný pohyb částic (molekul, atomů), je-li v některém místě vyšší koncentrace než v jiném místě. Otevřeme-li např. v jednom rohu uzavřené místnosti voňavku, za chvíli ji ucítíme i ve druhém rohu místnosti (a to i v případě, že v místnosti vzduch neproudí). Tomuto jevu říkáme difuze, je způsobena tepelným pohybem částic a v jednorozměrném přiblížení ji můžeme popsat jednoduchou rovnicí Q = -D.dn/dx, kde Q je počet částic prošlých jednotkovou plochou za jednotku času (proudová hustota, rozměr m^-2s^-1), D je difuzní koeficient (s rozměrem m²s^-1), n je koncentrace částic a x je rozměr, podél něhož difuzi studujeme. Vidíme, že Q je úměrné gradientu koncentrace; záporné znaménko nám říká, že proud částic směřuje proti směru vzrůstu koncentrace. Efekt difuze není nikterak omezen na plynná prostředí a existuje tedy i v pevných látkách. Je to právě difuze nosičů náboje se započítáním vlivu elektrického pole, na jejímž základě můžeme vysvětlit efekty vznikající v PN přechodu a většinu procesů v polovodičových součástkách vůbec.

Předpokládejme, že jsme vytvořili PN přechod tak, že nalevo od počátku (pro záporná x) máme polovodič typu p a napravo od počátku polovodič typu n. Majoritními nosiči náboje v typu n jsou elektrony, v typu p díry. Vytvořením PN přechodu jsme vlastně vytvořili gradient koncentrace elektronů, který v bodě x=0 má vysokou kladnou hodnotu a gradient koncentrace děr, který v bodě x=0 má vysokou zápornou hodnotu. Ihned po vytvoření přechodu nastane tedy difuze děr z polovodiče typu p do polovodiče typu n a difuze elektronů z polovodiče typu n do polovodiče typu p. Jakmile se majoritní nosiče jednoho druhu dostanou do prostředí, kde jsou majoritními nosiči nosiče opačné polarity, prakticky okamžitě zrekombinují, tedy zaniknou z hlediska vedení proudu. Majoritní nosiče, které předifundovaly do polovodiče opačné vodivosti však odkryly náboj iontů příměsí, které jsou vázány v krystalové mřížce a nemohou se proto pohybovat. Např. díry, které předifundovaly z polovodiče typu p do polovodiče typu n, ”zanechaly” po sobě v polovodiči typu n nezkompenzovaný náboj záporných iontů třímocných příměsí a obdobně elektrony ”zanechaly” po sobě v polovodiči typu n nezkompenzovaný náboj kladných iontů pětimocných příměsí. Znamená to, že další a další difuze majoritních nosičů přes přechod se děje pod vlivem elektrického pole, neboť záporné ionty příměsí na straně polovodiče typu p působí svým přitažlivým elektrickým polem na difundující díry a obdobným efektem působí kladné ionty příměsí na straně polovodiče typu n na difundující elektrony. To má za následek, že po určité době se vytvoří rovnovážný stav a ten je právě charakterizován nedeformovanou Fermiho hladinou přes přechod PN. Je třeba si uvědomit, že celkový náboj v polovodiči zůstává zachován, tak že polovodič zůstává navenek elektricky neutrální, zmíněný přesun náboje probíhá jen v bezprostřední blízkosti přechodu PN. Kdybychom tedy připojili voltmetr na konce našeho jednorozměrného krystalu s PN přechodem, nenaměříme voltmetrem žádné napětí.

Zatím jsme diskutovali jen majoritní nosiče. Jejich pohybem vznikají vázané náboje iontů příměsí a tedy elektrické pole bránící další difusi majoritních nosičů. Jak je to však s minoritními nosiči? Ty mají opačný náboj než majoritní nosiče a vzniklé elektrické pole tedy urychluje transport minoritních nosičů přes PN přechod. Rozmyslete si, že je to skutečně tak; brzdí-li vytvořené elektrické pole např. pohyb děr ”zprava doleva”, pak jistě pohyb elektronů zprava doleva bude tímtéž polem podporován. V analogii s gravitačním polem díry zprava doleva musí ”do kopce”, zatímco elektrony zprava doleva to mají ”s kopce”. Elektrické pole v oblasti přechodu tedy ”odsává” minoritní nosiče přes přechod, čímž vzniká gradient koncentrace minoritních nosičů v blízkosti přechodu, který ”se stará” o to, aby minoritní nosiče z míst vzdálenějších přechodu k němu difundovaly. Vznikne opět rovnovážný stav, kdy proud děr jako majoritních nosičů z typu p do n je kompenzován proudem děr jako minoritních nosičů z n do p a obdobně pro elektrony. Vidíme, že minoritní nosiče zde plní velmi významnou úlohu kompenzace zbytku proudu majoritních nosičů (z chvostu distribuční funkce), které se přece jenom přes vytvořenou potenciálovou bariéru dostanou.

Důležité je si uvědomit, že proud minoritních nosičů je nasycený, tj. elektrické pole v oblasti přechodu PN je natolik velké, že stačí odsát všechny minoritní nosiče, které se do blízkosti přechodu dostanou (podíváte-li se o několik odstavců výše, uvidíte, že tento proud je dán difusním koeficientem minoritních nosičů příslušného druhu a gradientem jejich koncentrace; tento gradient však nemůže být příliš veliký, neboť koncentrace minoritních nosičů je malá a proto ani celkový difuzní proud nebude velký). Z toho plyne, že tento nasycený proud minoritních nosičů nebude prakticky záviset na výšce potenciálové bariéry mezi stranou p a stranou n.

Přiložíme-li nyní na PN přechod napětí v takové polaritě, že strana p je kladná a strana n záporná (tzv. propustný směr), budeme působit naším vtištěným elektrickým polem proti elektrickému poli, které se přes přechod vytvořilo a tedy budeme vytvořenou difuzní potenciálovou bariéru snižovat. Uvážíme-li tvar Maxwell- Boltzmannovské rozdělovací funkce budeme tím exponenciálně zvyšovat počet majoritních nosičů z obou stran, které se přes bariéru dostanou. Přitom, jak jsme si uvedli, proud minoritních nosičů nebude touto naší akcí významně ovlivněn. Přiložíme-li napětí v opačné polaritě (tzv. závěrný směr), budeme naopak potenciálovou bariéru, která brání průchodu majoritních nosičů přes přechod zvyšovat a počet majoritních nosičů přes přechod se bude (opět exponenciálně) snižovat. Opět při této akci neovlivníme významně množství minoritních nosičů, které se přes přechod dostávají. To znamená, že při dostatečně vysokém napětí této polarity zmenšíme proud majoritních nosičů prakticky na nulu a přes přechod poteče pouze proud minoritních nosičů. Snadno se dá odvodit tzv. diodová rovnice,

I=I_o(exp(eV/kT)-1),

kde V je napětí na přechodu (kladné v propustném směru) a I_o tzv. zbytkový proud. Při odvozování této rovnice je třeba předpokládat, že veškeré z vnějšku přiložené napětí se objeví na přechodu, jinak řečeno, že proudy v propustném směru budou tak malé, aby nezpůsobily ohmické úbytky při průchodu proudu polovodičem od kontaktu k přechodu. Zhruba se dá říci, že to je splněno pro proudy až do cca 1 mA a v tomto rozmezí proudů může tedy dioda sloužit jako prvek s exponenciální voltampérovou charakteristikou. Pro vyšší proudy pak ohmické úbytky převáží, uvedená diodová rovnice přestává platit a je nahrazena prostým Ohmovým zákonem, kde v roli odporu vystupuje odpor materiálu diody (představíme-li si odpor materiálu diody a odpor přechodu jako dva odpory v serii, pak při malých proudech bude odpor přechodu podstatně větší než materiálu a bude záviset na napětí, při vyšších proudech se odpor materiálu podstatně nezmění a odpor přechodu klesne v podstatě na nulu). VA charakteristika reálné diody je na obr. 3.12a.

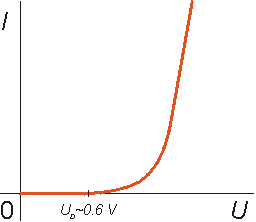
obr. 3.12a

Kapacitní dioda - varikap