| X | Y | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
7.3. Kombinační logické systémy
Elektronické obvody, které realizují logické funkce dělíme do základních dvou skupin: na tzv. kombinační a sekvenční logické systémy. První skupina (logická hradla) je charakterizována tím, že výstupní stav systému závisí pouze na okamžitých stavech (kombinaci) vstupních logických proměnných; při jejich změně dochází ke změně výstupního stavu se zpožděním, daném jen dobou průchodu signálu přes použité elektronické obvody. Sekvenční logické systémy (systémy s mezipamětí, klopné obvody) generují výstupní stav na základě hodnoty vstupních logických proměnných a na základě předchozí hodnoty výstupu. Výstup těchto obvodů je tedy definován jen tehdy, je-li definována časová posloupnost (sekvence) změn vstupních hodnot; z toho též plyne jejich název. Probereme nejprve příklady kombinačních a pak sekvenčních logických systémů.
Kombinujeme-li hradla OR a AND, popsaná v předcházejícím odstavci, s invertorem, můžeme vytvořit celou řadu dalších logických funkcí, z nichž nejpoužívanější jsou NAND - tzv. Shefferova funkce a NOR - tzv. Pierceova funkce. Vytvoří se tak, že na výstup hradla AND event. OR připojíme invertor. Výsledné pravdivostní tabulky pak jsou:
NAND NOR
| X | Y | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| X | X | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Podle de Morganových zákonů bychom mohli vytvořit hradlo NAND připojením dvou invertorů na oba vstupy hradla OR:
![]()
Obdobně hradlo NOR lze vytvořit z hradla AND a dvou invertorů na vstupech:
![]()
Funkce NAND a NOR lze rozšířit na libovolný počet vstupních logických proměnných. Definice těchto funkcí si čtenář jistě snadno utvoří sám.
Všimneme si ještě tří složených logických funkcí, které pro svou důležitost jsou často realizovány jako jeden logický člen. Jsou to funkce EXCLUSIVE-OR nazývaná též neekvivalence, funkce EXCLUSIVE-NOR neboli ekvivalence, shodnost a funkce čtyř logických proměnných AND - NOR, zvaná také AND - OR - INVERT.
Funkci EXCLUSIVE - OR lze obecně definovat pro n logických proměnných. Tato funkce nabývá hodnoty 1 právě když existuje mezi n vstupními logickými proměnnými alespoň jedna, která má jinou hodnotu, než ostatní. Lze snadno dokázat (důkaz je přenechán čtenáři), že vyjádřena v Booleově algebře bude funkce EXCLUSIVE - OR mít tvar (A1,A2, ..., An jsou vstupní logické proměnné):
![]()
Zde jsme si rovněž zavedli značku pro označení této logické funkce. Aby nedošlo k záměně se značkou logického součtu, budeme v těchto skriptech užívat pro logický součet a součin pouze značek “ +” a “ .”.
Nyní si podrobněji rozebereme hradlo EXCLUSIVE-OR pro dvě vstupní logické proměnné. Je zřejmé, že rozšíření pro více logických proměnných by šlo provést např. tímto způsobem:
![]()
neboť existuje-li alespoň
jedna proměnná Ai pro kterou platí ![]() pro i = 1, 2, 3, ..., n-1, je součet na
pravé straně tohoto výrazu roven logické 1 nezávisle na
hodnotách ostatních sčítanců. Můžeme tedy vytvořit funkci
EXCLUSIVE-OR pro n proměnných pomocí hradel realizujících
tuto funkci pro dvě logické proměnné a hradel základních.
Jsou-li A, B vstupní logické proměnné, lze tuto funkci zapsat
jako
pro i = 1, 2, 3, ..., n-1, je součet na
pravé straně tohoto výrazu roven logické 1 nezávisle na
hodnotách ostatních sčítanců. Můžeme tedy vytvořit funkci
EXCLUSIVE-OR pro n proměnných pomocí hradel realizujících
tuto funkci pro dvě logické proměnné a hradel základních.
Jsou-li A, B vstupní logické proměnné, lze tuto funkci zapsat
jako ![]()
Čtenář si jistě druhou rovnost snadno ověří. Z posledního vztahu vyplývá zapojení hradla EXCLUSIVE-OR pomocí dvou hradel AND, dvou invertorů a hradla NOR - obr. 7.20. Význam schematických značek je na obr.7.22.
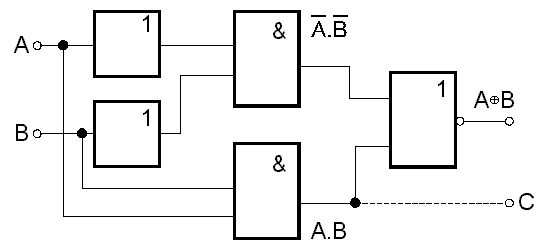
obr. 7.20
| A | B | A Ĺ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Důležitost funkce EXCLUSIVE-OR vyplyne z následující úvahy. Chtějme sečíst dvě binární čísla o jednom bitu. Výsledek nabude hodnoty 0 pakliže obě čísla budou 0 , hodnoty 1 je-li jedno z nich 0 a druhé 1. Jsou-li obě čísla rovna 1, pak součet bude opět 0, ale je potřeba vytvořit přenos do eventuálního následujícího bitu. Označíme-li součet S a přenos C (carry), pak je zřejmé, že
S = A Ĺ B
C = A . B
Obvodu generujícímu tyto dvě veličiny se říká polosčítačka a náležitá pozornost mu bude věnována později. Na obr. 7.20 je rovněž znázorněno, že jednoduchou úpravou (vyvedením jednoho ze vstupů hradla NOR) lze získat z hradla EXCLUSIVE-OR polosčítačku.
Ekvivalence je jak již název napovídá inverzní funkcí k právě popsané a lze ji jednoduše vytvořit přidáním invertoru k hradlu EXCLUSIVE-OR. Tohoto způsobu však není možno použít při návrhu složitějších logických sítí a vždy je nutno promyslet nejefektivnější způsob generace té které logické funkce, jinak by neúměrně narůstaly rozměry, příkon a ve zdaleka ne poslední řadě také cena příslušné logické sítě. Proto vztah pro tuto funkci upravíme:
![]()
Lze tedy snadno upravit schéma na obr. 7.20. buď užitím na výstupu hradla OR místo hradla NOR, nebo prostou změnou zapojení vstupů hradel AND jak je ukázáno na obr. 7.21. Toto zapojení je výhodné zejména tím, že vyvedením výstupů hradel
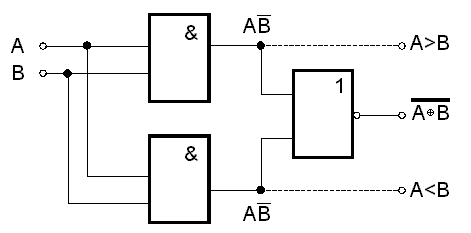
obr. 7.21
| A | B | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
AND získáme jednobitový
komparátor. Součin ![]() je totiž
roven 1 právě když A = 1 a B = 0 tj.A > B, stejně
je totiž
roven 1 právě když A = 1 a B = 0 tj.A > B, stejně ![]() je rovno 1 právě když A = 1 a B = 0,
tj. A < B. Výstup
je rovno 1 právě když A = 1 a B = 0,
tj. A < B. Výstup ![]() je roven 1 právě když
A = B = 0 nebo A = B = 1.
je roven 1 právě když
A = B = 0 nebo A = B = 1.
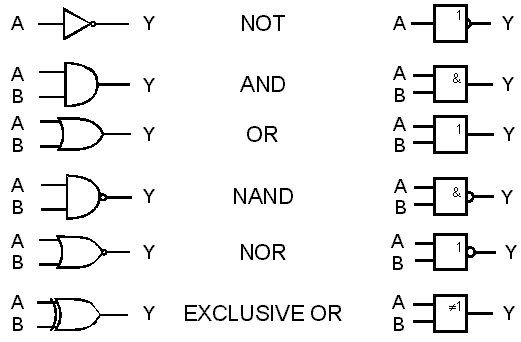
obr. 7.22
Hradla AND-OR-INVERT jsou logické obvody sestavené ze dvou hradel AND a z jednoho hradla NOR. Pravdivostní tabulka takového hradla je uvedena vlevo, schéma je na obr.7.23.
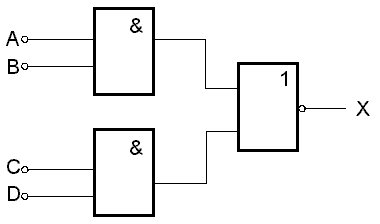
obr. 7.23
| A | B | C | D | X |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Vyjádření logické funkce je jednoduché. Je to:
![]()
Proč se tyto obvody vyráběly v integrované formě vyplyne nejlépe, porovnáme-li obrázek 7.23 s obr. 7.20 a 7.21. Z tohoto srovnání vidíme, že můžeme tímto obvodem za pomoci dvou invertorů vytvořit funkce EXCLUSIVE-OR/NOR a navíc propojíme-li oba vstupy každého u hradel AND, můžeme realizovat funkci NOR. Tato hradla se vyráběla pod označením 7450 a 7453.
Důležitými kombinačními logickými obvody jsou dekodéry, které slouží k převodu informace vyjádřené v jednom kódu na jiný. Jako příklad si zde uvedeme dekodér 1/N, který převádí slovo z binárního kódu na kód N proměnných, kde každá proměnná je vedena po samostatném vodiči. Principiální zapojení pro N = 4 je uvedeno na obr. 7.24 spolu s pravdivostní tabulkou.
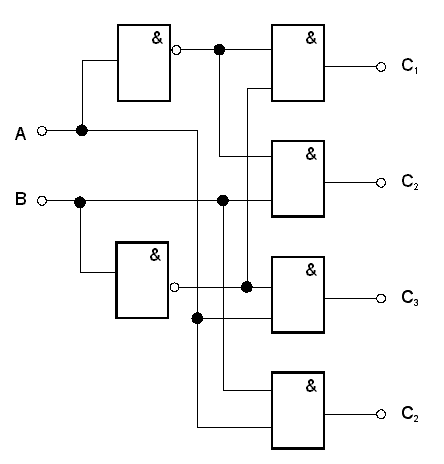
obr. 7.24
| vstupy | výstupy | ||||
| A | B | C1 | C2 | C3 | C4 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Schematické značky logických obvodů jsou uvedeny na obr. 7.22. Na levé straně jsou uvedeny značky starší, ještě však hojně používané, na pravé novější, přizpůsobené ke snadnějímu grafickému znázornění.
| Předmět a metody zjednodušování logických výrazů - Metody zjednodušování logických výrazů |