7.4.2. Algebraická metoda zjednodušování

Obecný postup se dá charakterizovat následujícím způsobem:

  1. Je třeba získat Booleovský výraz pro požadovanou logickou funkci buď z popisu nebo z pravdivostní tabulky nebo ze schématu logické sítě.
  2. Provést vlastní zjednodušení aplikací Booleovských identit, vytýkáním, substitucí apod.
  3. Porovnat výsledný vztah s původní pravdivostní tabulkou.

Při provádění úprav logických výrazů (ad 2) můžeme s výhodou využít tabulky 7.3., kde jsou uvedeny nejdůležitější identity platné obecně v Booleových algebrách.

T a b u l k a 7.3

Nejprve si vysvětlíme, jakým způsobem si sestavíme logický výraz, je-li dána pravdivostní tabulka. Obecně totiž může být logická funkce zadána tabulkou, popisem nebo zapojením logických členů. Je-li logická funkce zadána popisem, snadno sestrojíme z popisu pravdivostní tabulku nebo přímo Booleovský výraz. Pokud bychom vycházeli z daného zapojení logické sítě, není jistě složité odvodit logický výraz ze zapojení. Pokud máme pravdivostní tabulku, překreslíme ji nejprve tak, aby obsahovala jak vstupní proměnné, tak jejich komplementy. Pak si všímáme jen řádků, ve kterých má výsledek nabýt logické jedničky a napíšeme součin všech vstupních proměnných nebo jejich komplementů, které nabývají v tomtéž řádku hodnoty 1. Tento postup opakujeme pro všechny řádky, pro které je výstup roven 1. Například pro 3 vstupní logické proměnné máme dánu tabulku vlevo:

Tu přepíšeme užitím rovněž negovaných vstupních proměnných (vpravo):

A B C Y
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
A B C Y
0 1 0 1 0 1 0
0 1 0 1 1 0 1
0 1 1 0 0 1 1
0 1 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 1 1 0 0
1 0 1 0 0 1 0
1 0 1 0 1 0 1

Logický obvod je znázorněn na obr. 7.25.a.

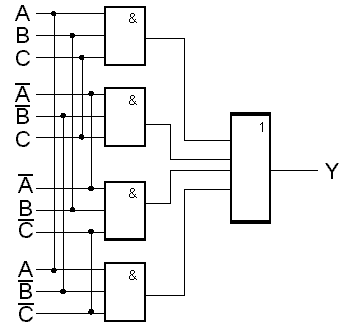
obr. 7.25a

Nyní uplatníme své znalosti identit platných  Booleově algebře. Na výraz

uplatníme zákon komutativní

vytkneme C event.

a použijeme identity

Substituce

,

zjednoduší výraz na

.

Použitím definice funkce EXCLUSIVE-OR získáme nakonec

 

Funkci Y tedy reprezentují dvě hradla EXCLUSIVE-OR zapojená v kaskádě jak je ukázáno na obr. 7.25.b. Funkce Y je též příkladem kombinačního logického systému.

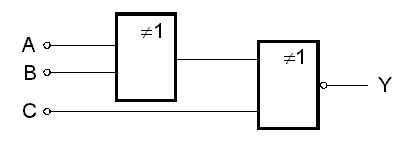
obr. 7.25b

Uvedený příklad nebyl vybrán náhodně. Reprezentuje obvod pro generaci, případně kontrolu tzv. parity. Parita je jednoduchý způsob odhalení chyby při přenosu dat. Zakládá se na předpokladu, že pravděpodobnost výskytu chyby při přenosu je velmi malá, a pokud tedy k chybě dojde, bude pouze v jednom z přenesených bitů. Kontrola paritou spočívá v přidání dalšího, tzv. paritního, bitu k přenášeným bitům tak, aby celkový počet jedniček v přenášeném slově (například bytu) spolu s paritním bitem byl sudé nebo liché číslo. Na přijímací straně se pak paritní bit jednak přečte, jednak vygeneruje, a komparátorem porovná; jsou-li oba případy stejné, přeneslo se dané slovo správně (de-facto víme jen, že nenastala chyba v lichém počtu bitů, pokud by došlo k chybě ve dvou, čtyřech, atd. bitech, parita ji neodhalí; proto je nutný předpoklad o spolehlivosti přenosu). Konstruujeme-li paritní bit tak, aby šlo o liché číslo, hovoříme o liché paritě, v opačném případě o sudé paritě. V našem případě je paritní bit volen tak, aby celkový počet jedniček v daném čtyřbitovém slově byl sudý. Jedná se tedy na vysílací straně o generátor, případně, na straně přijímače, o ověřovač sudé parity. S paritou se setkáváme při nastavování seriových rozhraní osobního počítače, při komunikaci pomocí modemu apod.

Další ... Sekvenční logické systémy