Příklad:

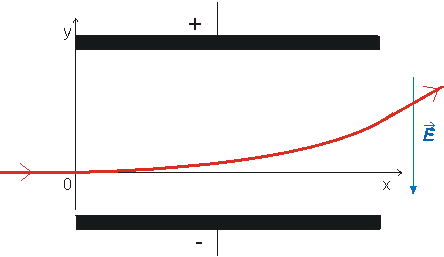
Jak se zakřiví (jaká bude rovnice trajektorie) dráha elektronu prolétajícího rychlostí 1.10⁷ ms^-1 mezi vychylovacími destičkami , které jsou 10 cm dlouhé? Mezi destičkami je el. pole o intenzitě 1.10³ Vm^-1.

Řešení:

Ve směru osy x se elektron pohybuje stále stejnou rychlostí v_x, tedy za čas t urazí dráhu x = v_xt. Ve směru osy y na něho působí síla o velikosti F_y = eE, kde e je náboj elektronu a E je velikost intenzity el. pole mezi deskami. Můžeme napsat pohybovou rovnici ma_y = eE, z čehož je . Za čas t tedy elektron urazí ve směru y dráhu . 

Souřadnice elektronu v čase t jsou popsány dvěma rovnicemi:
x = v_xt

Vyloučením t z těchto dvou rovnic dostaneme obecnou rovnici trajektorie (tedy závislost y na x) 

.

Toto je rovnice paraboly - elektron se mezi deskami pohybuje po parabolické trajektorii. Mezi destičky vletí v bodě [0, 0] a vyletí v bodě s x=10 cm, tedy

Elektron vyletí po zakřivené dráze o 0,88 cm výše než na začátku destiček. Jeho další dráha svírá s původním vodorovným směrem úhel a = 10º (abyste mohli tento úhel spočítat, je nutno umět počítat směrnice tečen).

Verze pro tisk