| 3.1.1. Periodické potenciály a energetické pásy v pevné látce |
Atomy v pevné látce jsou uspořádány v prostorové mřížce, která se periodicky opakuje. Pohybuje-li se elektron jako nosič náboje touto periodickou strukturou, ”vidí” potenciály jednotlivých atomů a pokud se dostane do blízkosti některého z jader, ”pocítí” odpudivou sílu, která mu nedovolí se do blízkosti jádra přiblížit. V oblasti mezi atomy bude elektron pod vlivem přitažlivého coulombického potenciálu, neboť tento potenciál ubývá, jako síla dalekého dosahu, pomalu jako 1/r. Pokud jsou atomy dostatečně blízko sebe, může elektron ”vidět” coulombické potenciály od několika různých jader současně, jinými slovy příspěvky coulombického potenciálu od různých jader se skládají a vytvářejí kombinovaný potenciál, který pak popisuje sílu působící na elektron.
Pro zjednodušení situace si prostorové periodické uspořádání atomů v krystalu látky představujeme jen v jedné souřadnici - jednorozměrně. Musíte mi věřit, že i tento velmi zjednodušená představa vede k velmi solidnímu popisu dějů spojených s vodivostí v pevných látkách. V jednorozměrném přiblížení budou jádra atomů jednoduše rozmístěna periodicky po ose úseček (černé tečky) a na osu pořadnic vynášejme průběh potenciálu. Obr. 3.1.
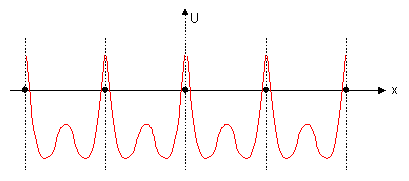
obr. 3.1.
Abychom porozuměli průběhu potenciálu, uvědomme si, že derivace (strmost se znaménkem) potenciálové křivky představuje intenzitu elektrického pole a že tedy síla působící na elektron je přímo úměrná této derivaci (s opačným znaménkem). Strmé části křivek v blízkosti jader představují potenciál odpudivých sil od jádra, které rychle klesají se vzdáleností (síly krátkého dosahu) a v určité vzdálenosti od jádra již existuje jen složený (zde od dvou jader) přitažlivý coulombický potenciál. V osamoceném atomu se elektron pohybuje ”někde” v potenciálovém ”příkopu” vytvořeném složením odpudivého potenciálu jádra a přitažlivého coulombického potenciálu. I když toto bude částečně pravda i v našem případě lineární mřížky, vidíme, že coulombické potenciály od dvou sousedních jader se skládají a vytvářejí ”vlnku” s maximem nižším než nula (coulombický potenciál je v nekonečnu nula a má-li být síla přitažlivá, musí potenciál směrem k jádru klesat do záporných hodnot; teprve v blízkosti jádra vlivem superpozice s potenciálem odpudivých sil vzroste potenciál nad nulu). Pokud je tedy elektron na vyšší energetické hladině, má šanci cestovat periodickou strukturou, jinými slovy přestává být lokalizován ke ”svému jádru”. Bystrá čtenářka již jistě odhalila problém - jak se může pohybovat elektron ve směru osy x od jednoho jádra ke druhému, když mu v cestě stojí odpudivé potenciálové bariéry v blízkosti jader? Odpověď dává tzv. tunelový efekt (řeší se v kvantové mechanice), který umožňuje částici s energií E ”protunelovat” potenciálovou bariéru s amplitudou vyšší než E za předpokladu, že bariéra je ”tenká”. Vzhledem k tomu, že síly odpuzující elektron od jádra jsou síly krátkého dosahu, je přirozené předpokládat, že bariéra tvořená potenciály těchto sil v našem jednorozměrném případě je velmi tenká, a že tedy elektrony mají značnou šanci protunelovat od jednoho jádra ke druhému, tedy být ”delokalizovány”. To však, jak hned ukážeme, ještě neznamená, že mohou vést proud.
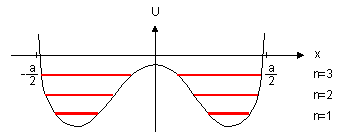
obr. 3.2a
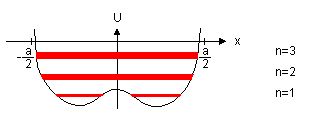
obr. 3.2b
Jsou-li atomy osamocené, nebo dostatečně daleko od sebe, nepůsobí prakticky na sebe, elektrony jsou lokalizovány v blízkosti ”svých” jader a jejich energie jsou diskrétní hladiny, obdobně, jako to pro atom vodíku budete počítat v kvantové mechanice, viz obr. 3.2a. Přibližujeme-li atomy k sobě, ruší se částečně coulombické přitažlivé síly a elektrony přestávají být lokalizovány, viz obr. 3.2b. Tento efekt vzrůstá s dalším přibližováním atomů a stále více a více elektronů přestává být lokalizováno ke svým původním jádrům. Přitom dochází k ”rozmazání” diskrétních energetických hladin na pásy, což je důsledek tzv. Pauliho vylučovacího principu, který říká, že nemohou existovat dva elektrony ve stejném kvantovém stavu. Pokud je atom osamocený, nastává tzv. degenerace energetických hladin, tj. situace, kdy několik elektronů v různých kvantových stavech obsazuje energetickou hladinu o téže energii. Působením vnějšího pole (v našem případě coulombickou interakcí ostatních jader) se degenerace tzv. snímá a energetické hladiny se štěpí na tolik podhladin, aby každému stavu elektronu příslušela (o něco málo) různá energie. Velikost rozštěpení hladin je závislé na intenzitě vnějšího pole a tedy na vzdálenosti atomů od sebe. Můžeme si tedy velmi schematicky tento efekt znázornit tak, jak je uvedeno na obr. 3.3. Na ose x je vzdálenost atomů od sebe v mřížce, na ose y energie. Provedením ”řezu” přes rozštěpené energetické hladiny pro x rovné (lineární) mřížkové konstantě získáme tzv. energetický pásový diagram tak, jak jej budeme pro náš výklad v dalším používat. Vidíme, že energetické pásy (intervaly) energií, které mohou elektrony nabývat (vyšrafované), mohou být odděleny tzv. pásy zakázaných energií, zakázanými pásy.
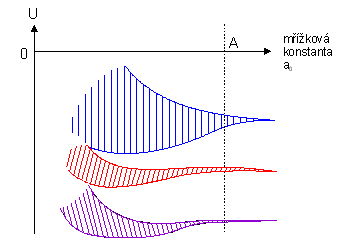
obr. 3.3
Pro vedení elektrického proudu v pevné látce jsou rozhodující dva pásy. Směrem od nejnižších energií poslední plně obsazený pás a následující zcela prázdný pás. Vysvětleme si nyní, proč tomu tak je. Elektrony jsou částice, které, jak jsme si již řekli, poslouchají Pauliho vylučovací princip. Představme si, že jste Stvořitelem a že tvoříte svůj první atom při teplotě absolutní nuly. Elektrony budou postupně zaplňovat energetické hladiny počínaje od té nejnižší, ale na té nemůže být nekonečný počet částic (to by bylo v případě bosonů, částic s celočíselným spinem), a proto se budou postupně obsazovat i další energetické hladiny až se dostaneme do situace, kdy nám dojdou elektrony. V atomu pak budou za teploty absolutní nuly obsazeny energetické hladiny od té, co odpovídá nejnižší energii až po určitou energii. Hladiny odpovídající energiím vyšším zůstanou prázdné. Obdobně je tomu i v pevné látce, tam se ale postupně zaplňují pásy povolených energií až zaplníme ten nejvyšší a nad ním už další možné pásy zůstanou volné. Může se taky stát, že nejvyšší pás nezaplníme zcela; diskusi tohoto případu si však ponecháme až nakonec, nyní probereme případ, že při teplotě absolutní nuly máme určitý počet pásů dovolených energií úplně zaplněných. Poslednímu zaplněnému pásu budeme říkat valenční pás, dalšímu nad ním vodivostní pás. Mezi valenčním a vodivostním pásem je interval zakázaných energií, tzv. zakázaný pás. Šířka tohoto intervalu zakázaných energií, zkráceně budeme říkat šířka zakázaného pásu je rozhodující pro vodivost látky. Ohřejeme-li nyní látku na pokojovou teplotu, dodáme tím elektronům v látce určitou energii. Obdobně jako je tomu u ideálního plynu, nebudou mít všechny elektrony stejnou energii, ale energie náhodně vybraného elektronu bude popsána tzv. rozdělovací funkcí elektronů podle energie (u molekul ideálního plynu se jedná o tzv. Maxwellovo-Boltzmannovo rozdělení). Tato rozdělovací funkce nám vyjadřuje pravděpodobnost, že náhodně vybraný elektron bude mít energii v předem stanoveném intervalu od E do E+dE. Z toho, jak jsme si popisovali obsazení energetických pásů elektrony za teploty absolutní nuly plyne, že tato funkce má hodnotu rovnou jedničce až do určité energie a nad ní má hodnotu rovnou nule. Tuto energii pod níž při teplotě absolutní nuly jsou všechny povolené energetické hladiny obsazeny, a nad níž jsou všechny povolené energetické hladiny prázdné, nazýváme Fermiho energií. Poznamenejme, že definice rozdělovací funkce je formulována tak, že rozdělovací funkce existuje i pro energie, které jsou v dané látce pro elektrony zakázány; pojem rozdělovací funkce se vztahuje k popisu energií elektronů a nikoliv k dané látce. Pokud bychom měli látku, ve které by žádné intervaly zakázaných energií neexistovaly, tak by obsazení energetických hladin elektrony bylo popsáno stejnou rozdělovací funkcí jako v našem modelu, kde zakázané pásy předpokládáme.
Uvažme, jak se může ”pravoúhlý” charakter našeho rozdělení energií změnit při zahřátí látky. Z názoru plyne (někdy je názor zavádějící, ale nikoliv v tomto případě), že zahřátí látky neovlivní nikterak podstatně elektrony obsazující nejnižší energetické hladiny; aby tyto elektrony mohly ”přijmout” tepelnou energii, musely by mít možnost přejít na vyšší energetickou hladinu, tuto možnost ale nemají, neboť hladiny ”nad nimi” jsou obsazeny. Proto bude energetické rozdělení elektronů zahřátím modifikováno jen málo a bude se jednat v podstatě o zaoblení ”rohů” původně ”pravoúhlého” rozdělení. Určitou představu již tedy máme, a proto teď uvedu vzorec pro energetické rozdělení elektronů, obecněji pro nerozlišitelné částice s poločíselným spinem, tzv. Fermi-Diracovo rozdělení. Je dáno vztahem:
fFD(E)=(1+exp((E-EF)/kT))-1.
Vidíme navíc, že pro energii E=EF se pravděpodobnost obsazení Fermiho hladiny rovná 1/2. Na obr. 3.4. a,b vidíme průběh Fermi-Diracova rozdělení pro T=0 (obr. 3.4a) a pro T>0 (obr. 3.4b). Z toho intuitivně (což pro nás v tomto případě postačí) plyne, že leží-li Fermiho hladina v oblasti intervalu zakázaných energií mezi plně zaplněným valenčním a úplně prázdným vodivostním pásem, bude ležet za teploty absolutní nuly přesně v polovině zakázaného pásu. Výpočet tuto intuitivní představu potvrzuje.
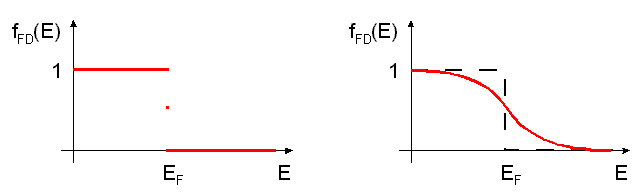
obr. 3.4a a 3.4b
Vraťme se nyní k popisu vodivosti v pevných látkách na základě faktů., která již známe a vysvětleme si nyní, proč jsou valenční a vodivostní pásy tak důležité pro tento popis. Představme si, že látku umístíme do elektrického pole. Elektrický proud je definován jako množství elektrického náboje, které projde plochou průřezu vodiče za jednotku času. Aby došlo k pohybu nosičů náboje v látce je třeba, aby došlo k urychlení elektronů z klidu. Jinými slovy je třeba, aby elektrony získaly od elektrického pole energii. To však není možné, neboť valenční pás je plně obsazen a není v něm tedy jediná volná energetická hladina. Ty jsou až za pásem zakázaných energií, ve vodivostním pásu. Pro odhad vodivosti látky je tedy důležité vědět, zda ve vodivostním pásu jsou nějaké nosiče náboje, příp, odhadnout jejich koncentraci. Při teplotě absolutní nuly víme, že koncentrace elektronů ve vodivostním pásu je nulová. Ohřejeme-li látku na pokojovou teplotu, existují již ”v chvostu”, tj. vysokoenergetické části rozdělovací funkce elektrony, které mají energii potřebnou na překonání zakázaného pásu, jejich koncentrace však ubývá exponencielně se zvětšováním šířky zakázaného pásu, kterou budeme v dalším značit Eg (z anglického gap). Tento fakt plyne z uvedeného vztahu pro Fermi-Diracovo rozdělení pro případ E >> EF; EF zanedbáme vůči E a jedničku ve jmenovateli zanedbáme vůči exponenciele a dostáváme přibližný vztah pro naši podmínku vyšších energií fFD » exp(-E/kT). Tento vztah je (až na normalizační konstantu) totožný s Maxwellovským-Boltzmannovským rozdělením (fMB(E)) pro ideální plyn, obecněji s klasickým rozdělením pro rozlišitelné částice. Počet elektronů s energií větší než Eg najdeme jednoduše integrací tohoto vztahu od Eg do nekonečna a dostaneme obdobnou exponencielní závislost, jen místo E bude v exponentu Eg (zkuste si to). Počet elektronů, které jsou schopny dostat termickou excitací přes pás zakázaných energií, tedy exponencielně klesá se zvětšující se šířkou zakázaného pásu. Exponenciele exp(-Eg/kT) se někdy říká Boltzmannův faktor (angl. Boltzmann factor). Složitější výpočet s pomocí kvantové mechaniky nám dává pro hustotu elektronů ve vodivostním pásu následující vztah:
n=(1/4)(8pme*.k.T/h2)3/2.exp(-(Ec-EF)/kT),
kde Ec je poloha (hodnota) spodní hranice vodivostního pásu, me* tzv. efektivní hmotnost elektronu a h Planckova konstanta. Znamená to, že pro látku se zakázaným pásem širokým Eg=1.09 eV (křemík) (bez příměsí a v tepelné rovnováze) bude hustota elektronů ve vodivostním pásu při pokojové teplotě (kT=28.7 meV) asi 1,5.1016 m-3.
Proč elektrony nemohou získat dostatečnou energii k překonání zakázaného pásu z elektrického pole? Vysvětlení tkví v úvaze, že pohybující se elektron může získávat energii jen na dráze, kdy neinteraguje s atomy v mříži, tj. na statistické střední volné dráze. Ta je v pevné látce v řádu 10-8 m a bylo by třeba pole o intenzitě cca 108 V/m, abychom elektron urychlili na pouhý jeden eV (elektronvolt) což je zhruba šířka zakázaného pásu pro křemík.
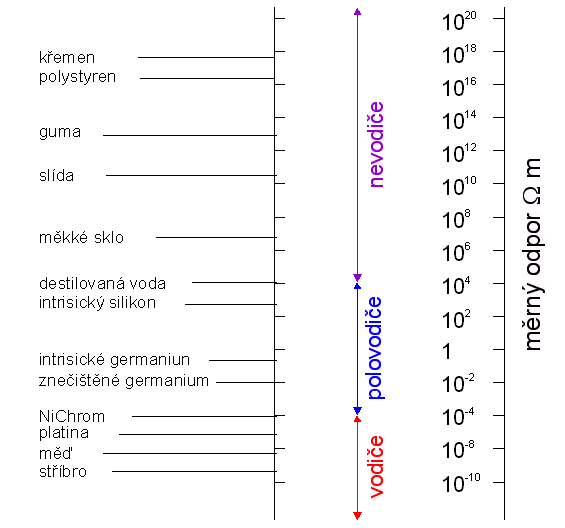
tab. 3.1
Na základě těchto znalostí již můžeme kvalitativně vysvětlit velmi rozdílnou elektrickou vodivost látek tak, jak je uvedena při pokojové teplotě v tabulce 3.1. Vidíme, že rozsah měrných odporů látek zahrnuje hodnoty od cca 1018 W.m u křemene až do hodnoty cca 10-9 W.m u stříbra, tedy 27 řádů. Uvědomíme-li si, že vodivost látky je úměrná koncentraci volných nosičů náboje a fakt, že tato koncentrace závisí exponenciálně na šířce zakázaného pásu, je kvalitativní vysvětlení nasnadě. Změna šířky zakázaného pásu o pouhých 56 meV způsobí e @ 3.7 násobnou změnu této koncentrace, zvětšení šířky zakázaného pásu o 1 eV způsobí zmenšení koncentrace nosičů danou faktorem 4.10-9. Je tedy zřejmé, že hlavní charakteristickou veličinou, která bude rozdělovat pevné látky na vodiče, polovodiče a izolanty, bude šířka zakázaného pásu.
Mezi izolanty řadíme látky se šířkou zakázaného pásu od cca 2-3 eV. Typický příklad pásové struktury izolantu vidíme na obr. 3.5., kde jsou, na rozdíl od obr. 3.3., zakresleny též energetické pásy. Ve srovnání s obr. 3.3. je obr. 3.5 nakreslen nikoliv pro hypotetickou substanci, ale pro chlorid draselný, KCl. Zakázaný pás této pevné látky má šířku cca 10 eV,
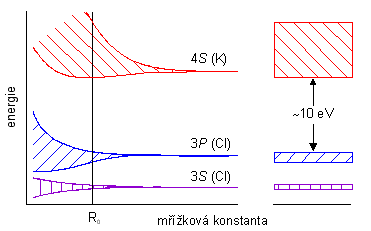
obr. 3.5
což odpovídá Boltzmannovu faktoru pro pokojovou teplotu v řádu 10-167 a znamená to, že ve vodivostním pásu chloridu draselného nemůže být za pokojové teploty prakticky žádný nosič náboje; proto je KCl velmi dobrý izolant.
Polovodiče se liší od izolantů pouze šířkou zakázaného pásu. Typickým představitelem a materiálem pro drtivou většinu polovodičových součástek je křemík se šířkou zakázaného pásu 1.09 eV, jehož pásová struktura je znázorněna na obr. 3.6. Příklady dalších polovodičů a šířek jejich zakázaných pásů: germanium (Ge), 0.72 eV, Galium arsenid (GaAs), 1.34 eV,
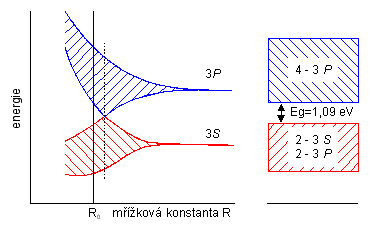
obr. 3.6
Indium antimonid (InSb), 0.18 eV, sirník kademnatý (CdS), 2.45 eV, oxid zinečnatý (ZnO), 3.3 eV. Základní charakteristické parametry křemíku a germania vidíme v tabulce 3.2. K tabulce se vrátíme později, nyní si všimněme pouze počtu atomů na m3 a tzv. vlastní (intrinsické) koncentrace nosičů náboje. Počet atomů na m3 se u obou polovodičů příliš neliší, ale vlastní koncentrace nosičů náboje se liší cca o 3 řády. To je dáno zejména rozdílem v šířce zakázaného pásu, který činí 0.37 eV.
U kovů neexistuje zakázaný pás mezi vodivostním a valenčním pásem, tyto dva pásy tvoří vlastně jeden ne zcela zaplněný pás. Na obr. 3.7. vidíme pásový diagram pro měď jako typický příklad kovu s dobrou elektrickou vodivostí.
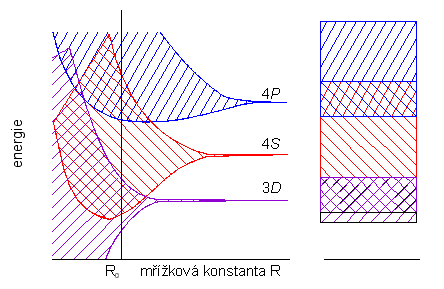
obr. 3.7
Pro vodiče v pevné fázi (kovy) tedy platí, že nemají zakázaný pás; proto jejich elektrony, je-li vodič vložen do elektrického pole, mohou být tímto polem urychleny, neboť existuje množství volných vyšších energetických hladin, na které mohou elektrony (se zachováním Pauliho principu) přejít. Proč tedy existují rozdíly mezi vodivostí jednotlivých kovů? Odpověď nám dá bližší pohled na přenos náboje v elektrickém poli, který je vysvětlen v následujícím odstavci.