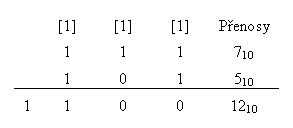
7.1.2. Aritmetické operace s binárními čísly
Pro sčítání binárních čísel platí stejné zásady jako pro sčítání čísel dekadických s tím, že přenos jedničky do vyššího řádu je generován nikoliv, když součet nabude hodnoty 10, ale nabude-li hodnoty 2 (1+1).
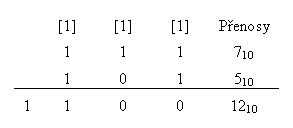
(součet v prvém sloupci odprava generuje jedničku přenosu, ta se sčítá s dalším sloupcem, čímž je generován další přenos a podobně ve třetím sloupci). Sčítání v digitálních počítačích probíhá v jednotkách zvaných sčítačky.
Pro odčítání bychom mohli zvolit tentýž algoritmus jaký používáme pro odčítání decimálních čísel. Je konstrukčně možné navrhnout a konstruovat odečítačku právě tak, jako je možné konstruovat sčítačku. V počítačích se však tento způsob nepoužívá, neboť je možné (pakliže najdeme vhodný způsob vyjádření záporných čísel) změnit znamení menšitele a provést operaci sčítání. Abychom si objasnili, jakým způsobem se v počítači záporná čísla vyjadřují, uvedeme si nejprve příklad z oboru čísel dekadických. Představme si mechanické počitadlo, např. počitadlo otáček u magnetofonu, řekněme 4-místné. Otáčí-li se cívka magnetofonu vpřed, počitadlo provádí operaci sčítání, otáčí-li se zpět, počitadlo příslušné otáčky odečítá. Představme si, že bychom potřebovali otočit cívku o 7 otáček zpět ve chvíli, kdy počitadlo ukazuje číslo 0004. Po každé otáčce zpět bude počitadlo ukazovat postupně
0004
0003
0002
0001
0000
9999
9998
9997
Počitadlo tedy neukazuje -3, ale číslo 9997, které tomuto zápornému číslu v 4-místném vyjádření odpovídá. Abychom si ověřili, sečteme třeba číslo 5 a 9997.
| 0005 |
| 9997 |
| (1)0002 |
Pakliže dodržíme počet míst (tedy 4), nemůžeme započítat poslední přenos a skutečně nám vyšlo číslo 2, což je výsledek odečtení 3 od 5. Číslo 9997 nazýváme doplňkem do desíti k číslu 3 ve čtyřmístném vyjádření. Pomocí doplňku do desíti můžeme v dekadické soustavě převést operaci sčítání na operaci odečítání.
Obraťme nyní pozornost k odečítání binárních čísel. Předpokládejme, že máme odečíst dvě kladná čísla (celá) o n bitech. Např. dvě čtyřbitová čísla (n = 4).
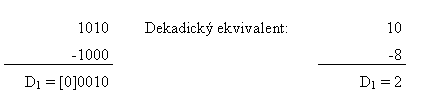
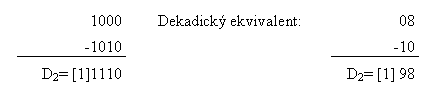
V prvém případě budeme předpokládat, že odečítáme menší číslo od většího . Přenos [0] z (n+1) bitu je nulový a rozdíl D1 je kladný. V případě, kdy odčítáme větší číslo od menšího 4bitové binární číslo 1110 označme Zn, [1] je přenos z (n + 1) bitu do n-tého bitu (je jednička) a rozdíl D2 můžeme napsat jako
D2 = -1*2n + Zn, (7.1)
kde první člen (-1.2n) na pravé straně je přenos (n + 1) bitu do nižšího a číslo Zn je n-bitové číslo výsledku odečítání. V našem případě
Zn = 1110
Protože pro jakékoliv číslo o n-bitech Zn platí
Z n < 2n,
je rozdíl D2 záporný a výraz (7.l) nám reprezentuje záporné číslo v binární soustavě.
Formálně můžeme přepsat pro první případ, tj. odečtení většího čísla od menšího, rozdíl D1 ve tvaru (kladné číslo):
D1 = -0*2n + Zn, (7.2)
a obecně
D1 = -A*2n + Zn, (7.3)
Ze vztahu (7.3) plyne, že přenos z (n + 1) do n-tého bitu ukazuje na to, zda je rozdíl záporný (A = 1) nebo kladný (A = 0).
Vraťme se nyní k případu záporného rozdílu
D = -1*2n + Zn,
Jeho velikost můžeme posoudit určením absolutní hodnoty
|D2| = 1*2n - Zn, (7.1)
O určení absolutní hodnoty záporného rozdílu D si můžeme vyslovit následující větu:
Absolutní hodnotu záporného rozdílu dvou binárních čísel
|D| = -1*2n + Zn
dostaneme tak, že v čísle Zn negujeme všechny bity (tj. za hodnotu 1 dosadíme 0 a naopak) a k nejméně významnému bitu přičteme 1.
Důkaz:
Nejvyšší číslo s n-bity je
2n - 1 = 1111 .....1 (celkový počet jedniček je n) (7.4)
Označme číslo Zn* , které nazveme doplněk do jedničky tak, že splňuje rovnici
2n - 1 = Zn + Zn* (7.5)
Ze vztahů (7.4) a (7.5) plyne, že číslo Zn* dostaneme jestliže negujeme všechny bity v Zn.
Absolutní hodnota záporného rozdílu se rovná
|D| = 1*2n - Zn
Přičtěme a odečtěme na pravé straně jednotku:
|D| = 1*2n - 1 - Zn + 1 = Zn* + 1
Protože Zn* dostaneme ze Zn tak, že všechny bity negujeme, je důkaz proveden.
Číslo
Zn´ = Zn* + 1
nazývám doplněk do 2 v n-místném vyjádření, protože pro něj platí
2n = Zn´ + Zn. (7.6)
Všimněme si, že v našem příkladu s počítadlem otáček u magnetofonu platí rovněž 3+9997=1000=104 (číslo 9997 je doplňkem do 10 ve čtyřmístném vyjádření). Obraťme nyní pozornost k vlastnímu odečítání. Předpokládejme, že máme odečíst dvě kladná binární čísla x a y
D = x - y (7.7)
Uvažujme součet
S = x + y' (7.8)
kde y' je doplněk do dvou čísla y. Podle definice o doplňku do 2 je
y' = y* + 1 = 2n - y. (7.9)
Dosadíme do ( 7.8 ) a obdržíme :
S = x - y + 2n = D + 2n
a pro rozdíl D z rovnice (7.7) dostaneme
D = S - 2n = x + y' - 2n. (7.10)
Ze vztahu (7.10) plyne, že rozdíl mezi binárními čísly x a y
D = x -y
obdržíme tak, že přičteme k číslu x doplněk do dvou čísla y. Od přenosu do n + 1 bitu odečteme podle (7.10) jedničku. Odečtení dosáhneme negováním přenosu. Pak pro výsledný přenos [1] je rozdíl záporný a pro přenos [0] je kladný.
K odečítání je tedy možné použít stejné technické prostředky jako při sčítání. Doplněk do 2 nám tedy umožňuje zobrazení záporných čísel v binární soustavě.
Nechť y je kladné číslo o délce n bitů. Pak zobrazení čísla (-y) můžeme provést následujícím způsobem:
Podle (7.6) platí
2n = y + y'
-y = - 2n + y' < 0. (7.11)
To znamená, že záporné čísla můžeme v binárním kódu zobrazit tak, že vytváříme k jeho absolutní hodnotě doplněk do dvojky. Skutečnost, že od doplňku je nutné odečíst podle vztahu (7.11) hodnotu -1.2n zobrazíme tak, že na n+1. bit píšeme 1. V případě kladného čísla je ovšem (n+1). bit nulový. Stejně jako ve vztazích (7.2) a (7.3) lze (n+1). bit považovat za “znaménkový bit”, kdy 1 značí minus a 0 značí plus. Jestliže zahrneme (n+1). bit do délky číselného slova, které má pak r = (n + 1) bitů a vytvoříme doplněk do dvojky celého slova o délce r, vytvoří se nám znaménkový bit automaticky pro určitý obor kladných a záporných čísel.
Předpokládáme, že máme mikropočítač s délkou slova 12 bitů, pak považujeme-li nejvyšší 12. bit za znaménkový, můžeme za použití notace s dvojkovým doplňkem zobrazit obor čísel podle tabulky 5.1.
TABULKA 5.1
| Binární kód | Desítkový ekvivalent | ||
| 0111 | 1111 | 1111 | +2047 |
| ....... | ....... | ....... | ....... |
| ....... | ....... | ....... | ....... |
| 0000 | 0000 | 0011 | +3 |
| 0000 | 0000 | 0010 | +2 |
| 0000 | 0000 | 0001 | +1 |
| 0000 | 0000 | 0000 | 0 |
| 1111 | 1111 | 1111 | -1 |
| 1111 | 1111 | 1110 | -2 |
| 1111 | 1111 | 1101 | -3 |
| ....... | ....... | ....... | ....... |
| ....... | ....... | ....... | ....... |
| 1000 | 0000 | 0000 | -2048 |
Násobení a dělení s binárními čísly se provádějí v počítačích obvykle podle stejného algoritmu jako v dekadické soustavě. Například :
| 5 | * | 3 | = | 15 | |||
| 0 | 1 | 0 | 1 | = | 510 | ||
| 0 | 0 | 1 | 1 | = | 310 | ||
| 0 | 1 | 0 | 1 | ||||
| 0 | 1 | 0 | 1 | ||||
| 0 | 0 | 0 | 0 | ||||
| 1 | 1 | 1 | 1 |
Je pochopitelné, že tímto způsobem můžeme spočítat pouze výsledky, které se dají vyjádřit příslušným počtem bitů, např. ve čtyřbitové reprezentaci je nejvyšším číslem právě číslo 15.
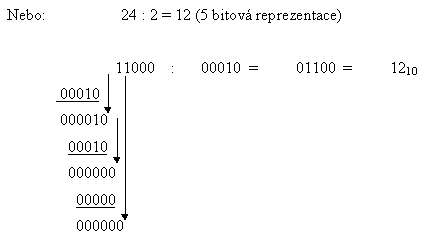
| Základní pojmy - Logické operace a jejich reprezentace elektronickými obvody |