7.2.3. Reprezentace základních logických funkcí elektronickými obvody
Obdobně jako při návrhu
lineárních obvodů je i číslicový obvod složen z řady
bloků, z nichž každý generuje specifickou logickou funkci.
Takový blok, který vytváří složitější logickou funkci
budeme nazývat logická síť a jednodušší logický obvod
reprezentující zpravidla logickou funkci dvou proměnných
budeme nazývat logickým
členem. Hranice mezi těmito dvěma pojmenováními však není
jednotná, zejména při návrhu složitějších logických
sítí je tendence označovat logickým členem i složitější
logický obvod např. více než dvou proměnných; v podstatě
se tohoto názvu často
užívá pro integrovaný obvod v jednom pouzdře. My se však v
těchto skriptech přidržíme zavedeného pojmenování.
Jak plyne z Booleovy algebry, je možné libovolnou logickou
funkci vyjádřit kombinaci logického součtu nebo logického
součinu a operace negace. Chceme-li tedy sestrojit obvod,
který by modeloval nějakou zadanou logickou funkci, musíme
mít k dispozici obvody, které generují uvedené základní
logické funkce. Elektronické obvody pro generaci uvedených
funkcí nazýváme po řadě: hradlo “OR”, hradlo “AND” a invertor. Zde
se budeme zabývat pouze nejjednoduššími obvody bez zřetele
na event. zatížitelnost, rychlost apod. Takovými obvody je
tzv. diodová logika DL- diode logic (přesněji řečeno
odporově - diodová logika). Dříve než si rozebereme schémata, je třeba vysvětlit pojmy
tzv. pozitivní a negativní logiky. Přiřazení logických
stavů “0” a “1” napěťovým úrovním je totiž
zcela libovolné a záleží na tom kterém přístroji, jakého
přiřazení používá. Pakliže stav logické “0”
odpovídá nižšímu napětí na výstupu logického členu
nežli stav logické “1”, hovoříme o tzv. pozitivní
logice. Je-li tomu naopak, tj. logické “0” odpovídá
vyšší napětí nežli logické “1”, pak se jedná
o negativní logiku. Přitom je třeba zdůraznit, že
nezáleží na velikosti napětí, obě mohou být kladná nebo obě
záporná nebo jedno kladné a druhé záporné; pakliže
logická “1” odpovídá kladnějšímu napětí, jedná se
o pozitivní logiku, jinak je to logika negativní. Stejným
způsobem se označuje logika tzv. dynamická (na rozdíl od
právě popsané
statické, neboli úrovňové logiky), kdy ovšem příslušné
úrovně jsou na vstupech logických členů pouze po velmi
krátkou dobu, tedy ve formě napěťových impulsů.
Vzhledem k tomu, že parametry reálného logického členu se
různí kus od kusu (užívají se odpory s určitou tolerancí,
tranzistory a diody, které mohou mít různé parametry), není
možné stanovit přesnou hodnotu napětí odpovídající
logické “0” resp. “1” v té které logické síti.
Místo toho se logické členy konstruují tak, aby nebyly
citlivé na změnu napětí
vstupních parametrů pokud tyto leží v určitém intervalu
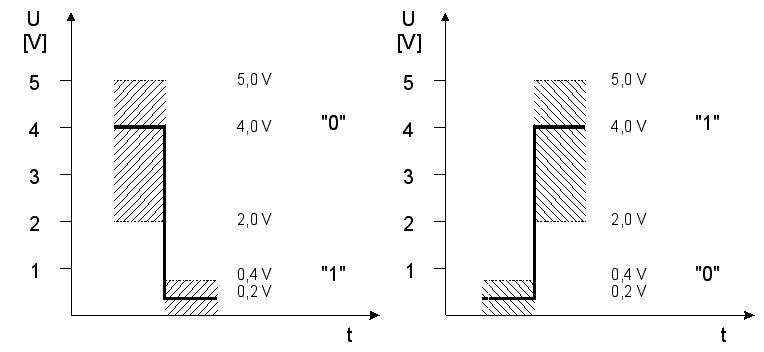
napětí. Viz obr.7.1.

obr. 7.1a a 7.1b
Například pro hradla TTL (transistor-transistor-logic) jsou příslušné intervaly následující:
Uvst(0) = max. 0,8 V
Uvst(1) = min. 2 V
neboli pro logickou “0” je povolený interval vstupních napětí 0 - 0.8V pro logickou “1” 2 - 5 V. Hradlo samo má zaručovaná výstupní napětí:
Uvýst(1) = min. 2,4 V
Uvýst(0) = max. 0,4 V
tj. hluboce v povolené toleranci napětí vstupních. Napájecí napětí je (5± 0,25) V. Uvedené hodnoty jsou typické pro tzv. tranzistorovou logiku a byly implementovány u celé řady výrobců logických obvodů. Zdaleka to však nejsou jediné napěťové úrovně u logických obvodů používané. Hradla s tranzistory řízenými elektrickým polem mají logické úrovně okolo 0 V a 9 V a existuje i tzv. logika s vysokou šumovou imunitou HLL (high-level-logic), kde napěťová úroveň logické “1” je řádu 10 - 50 V. S takovými napěťovými logickými úrovněmi pracují řídicí systémy v provozech, kde je zvýšená úroveň elektromagnetického rušení. Na druhé straně pro speciální přístroje s nízkým napájecím napětím (náramkové hodinky) byly vyvinuty obvody, kde jsou logické úrovně mezi 0 V a 3 V i níže.
Pokud nebude výslovně uveden opak, budeme se v těchto skriptech zabývat pouze pozitivní logikou. Podívejme se nyní na elektronickou reprezentaci hradla typu OR na obr. 7.2. Jak již bylo uvedeno, hradlo tohoto typu je vybaveno (na jeho výstupu je úroveň logické 1), je-li alespoň jeden z jeho vstupů vybaven.
| X | Y | X+Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
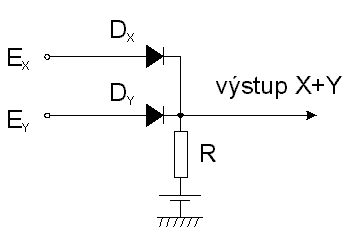
obr. 7.2
Jestliže předpokládáme ideální diody (tj. nekonečný odpor v závěrném směru a nulový v propustném směru), je funkce obvodu následující: Pro vstupní napětí Ex > e nebo Ey > e je odpovídající dioda otevřena a výstupní napětí kombinace je rovno Ex,y (předpokládáme-li, že zdroje napětí Ex,y i zdroj napětí e mají vnitřní odpor nulový). Je-li např. napětí Ex na vstupu X , pak dioda Dy je uzavřená, pokud napětí na vstupu Ey není větší než Ex. Pak se naopak zavře dioda Dx, vede Dy a výstup kopíruje napětí na vstupu Y.Všimneme-li si výstupního odporu tohoto hradla vidíme, že ve stavu logické 0 je roven odporu R, ve stavu logické 1 je nulový. Pokud používáme reálné diody a reálné zdroje napětí logických úrovní X a Y, musíme počítat s jejich vnitřním odporem ri, odporem diod v propustném směru a se zbytkovým napětím na diodách UD (u germaniových diod ~ 0,2V, u křemíkových ~ 0,7V). Zbytkové napětí na diodách má tu výhodu, že není třeba používat zdroj napětí, který nám předtím vytvářel oblast napětí pro úroveň logické 0 (logická 0 byla od 0V do e V), neboť diody se neotevřou, pokud vstupní napětí nepřekročí UD. Zahrneme-li odpor diod v propustném směru do vnitřních odporů zdrojů logických úrovní, bude při aplikaci napětí Ex = E napětí na výstupu rovno:
![]()
Jsou-li oba vstupy na úrovni E , bude výstupní napětí
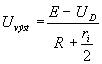
Výstupní odpor hradla bude ve stavu logické 1 roven
![]()
resp. ![]()
tedy pro
![]() je
je ![]() resp.
resp. ![]()
Vidíme, že i v takovémto
jednoduchém případě je nezbytné, aby logický člen
zpracovávající informaci z tohoto hradla byl necitlivý na
změnu úrovně logické 1 v rozmezí ![]() a logické 0 v rozmezí
a logické 0 v rozmezí ![]()
Elektronický model logického součinu funkce AND, je zobrazen na obr. 7.3 spolu s pravdivostní tabulkou. Funkci hradla lze z obrázku snadno odvodit; připomeňme jen, že u tohoto hradla je výstupní odpor roven R při úrovni logické jedničky (tedy naopak než u diodového hradla OR) a bude roven vnitřnímu odporu diody (resp. jeho polovině) ve stavu logické 0. Je tedy výstup hradla vysokoohmový ve stavu logické 1 a nízkoohmový ve stavu logické 0; naopak než u diodového hradla OR. Podobně jako v případě hradla OR si čtenář může ověřit platnost zákonů agresivnosti a neutrálnosti.
Je nasnadě, že vzhledem k platnosti zákona asociativního pro konjunkci i disjunkci lze výrazy
X = A1 A2 A3 A4 ..... An a Y = B1 + B2+ B3+ B4+ ..... + Bn
považovat za smysluplné. V prvém případě bude X rovno 1 právě když všechny logické proměnné Ai budou rovny 1 , ve druhém případě bude Y rovno 1 právě když alespoň jedna logická proměnná Bi, bude rovna 1. Je rovněž zřejmé, že u schémat uvedených na obr. 7.2 a 7.3 lze zvětšit počet vstupů hradel prostým zvětšením počtu příslušných vstupních diod.
| X | Y | XY |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
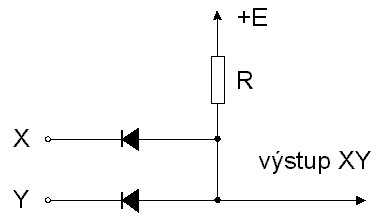
obr. 7.3
Funkci logické inverze
“NOT” je možno vytvořit transistorovým zesilovačem,
pracujícím ovšem ne v lineárním, ale ve spínacím režimu.
Je zřejmé, že zapojíme-li tranzistor do obvodu podle obr. 7.4
a budeme-li zvětšovat proud do jeho báze, bude jeho
kolektorové napětí klesat tak, jak to odpovídá jeho
výstupním charakteristikám a zatěžovací přímce. Od
určitého proudu báze však zjistíme, že napětí UKE
se prakticky nesnižuje -
transistor je ve stavu nasycení. Je to stav, kdy jak emitorový
přechod, tak kolektorový jsou pólovány v propustném směru,
a napětí mezi kolektorem s emitorem je v podstatě dáno
rozdílem napětí na přechodu báze-emitor a na přechodu
báze - kolektor.
Prakticky u křemíkového tranzistoru je toto tzv. saturační
napětí Usat
řádu 0,2 V a u germaniového tranzistoru řádu 0,1 V. Báze
je při tom nasycena minoritními nosiči náboje a veškerý
přírůstek proudu báze jde na úkor přírůstku proudu
emitoru. Při zvyšování kolektorového proudu Usat roste; tuto závislost lze aproximovat
přímkou a její směrnice se nazývá saturační odpor Rsat. Tato přímka neprochází
počátkem; její rovnice je ![]() , kde
, kde ![]() závisí na
vlastnostech tranzistoru; je obvykle
závisí na
vlastnostech tranzistoru; je obvykle ![]() . Přestaneme-li dodávat proud do
báze tranzistoru, uzavřou se obě diody (BE, BK) a přebytek
minoritních nosičů v bázi je opět odsáván el. polem v
oblasti kolektorového přechodu. Je zřejmé, že čím více
minoritních nosičů bylo v bázi před vypnutím, tím déle
bude trvat, než kolektor odsaje všechny minoritní nosiče v
bázi a kolektorový proud klesne na nulu. Proto je vhodné
zabezpečit, aby tranzistor
. Přestaneme-li dodávat proud do
báze tranzistoru, uzavřou se obě diody (BE, BK) a přebytek
minoritních nosičů v bázi je opět odsáván el. polem v
oblasti kolektorového přechodu. Je zřejmé, že čím více
minoritních nosičů bylo v bázi před vypnutím, tím déle
bude trvat, než kolektor odsaje všechny minoritní nosiče v
bázi a kolektorový proud klesne na nulu. Proto je vhodné
zabezpečit, aby tranzistor
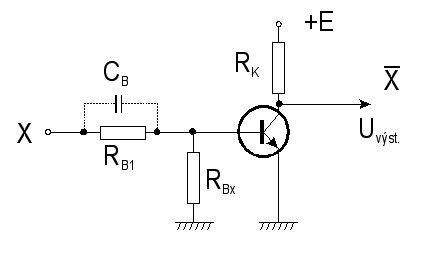
obr 7.4a
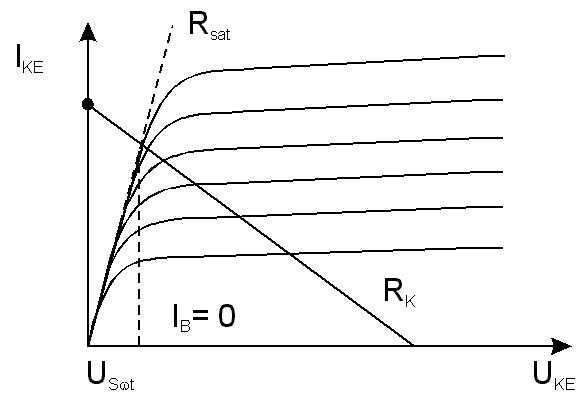
obr. 7.4b
v sepnutém stavu pracoval na
okraji oblasti nasycení: to lze dosáhnout např. použitím
tzv. desaturačních diod (viz další odstavec), zapojených
mezi bázi a kolektor. Kondenzátor CB
napomáhá urychlení
přechodového procesu odstranění minoritních nosičů
z báze, když měníme napětí vstupu z 1 na 0. Funkce obvodu
na obr. 7.4 je tedy následující: při aplikaci napětí
o logické úrovni 1 na vstup X invertoru zvětšíme proud
báze natolik, že tranzistor uvedeme do saturace. Na
výstupu ![]() je tedy napětí Usat,
které je obvykle 1/4 až 1/3 povoleného rozsahu napětí pro
logickou 0. Přivedeme-li na vstup zařízení napětí
o logické úrovni 0, je tranzistor vypnut a na jeho kolektoru
(tedy na výstupu invertoru) je plné napájecí napětí volené
tak, aby odpovídalo úrovni logické 1. Obvod tedy plní
logickou funkci negace.
je tedy napětí Usat,
které je obvykle 1/4 až 1/3 povoleného rozsahu napětí pro
logickou 0. Přivedeme-li na vstup zařízení napětí
o logické úrovni 0, je tranzistor vypnut a na jeho kolektoru
(tedy na výstupu invertoru) je plné napájecí napětí volené
tak, aby odpovídalo úrovni logické 1. Obvod tedy plní
logickou funkci negace.