5.3.2. Analogová derivace
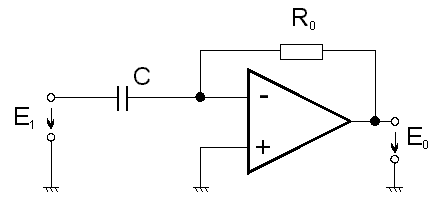
Analogový derivátor dostaneme modifikací zapojení základního integračního obvodu uvedeného na obr. 5.2.b. Základní zapojení analogového derivátoru je na obr. 5.15. Z obr. 5.15 plynou pro operátorové impedance výrazy:

obr. 5.15
Z1 = 1/pC a Z0 = R0;
![]()
a originál je dán výrazem:
![]()
Prakticky se však uvedeného zapojení nepoužívá, neboť derivátor má obrácenou frekvenční charakteristiku než integrátor a při derivování se zesiluje napětí tím více, čím má vyšší frekvenci.
Jestliže zesilujeme signál o frekvenci w , pak můžeme v symbolické formě psát:
![]() ; (5.11)
; (5.11)
to znamená, že zesílení analogového derivátoru se zvětšuje přímo úměrně s frekvencí derivovaného signálu. Tato skutečnost vede k podstatnému zhoršení poměru signál-šum na výstupu derivačního obvodu.
Pokud se nelze derivování vyhnout, používá se upravených obvodů, které omezují zesílení na vyšších kmitočtech. Jedním z používaných obvodů je kombinace derivačního a integračního obvodu uvedená na obr. 5.16.
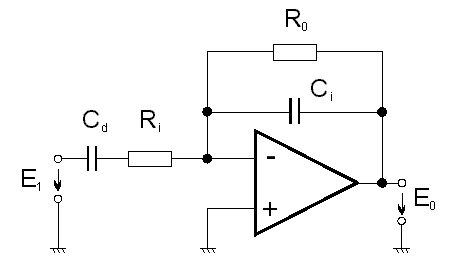
obr. 5.16
Jestliže zvolíme
t = RiCd = RdCi
pak napětí na výstupu je v závislosti na kmitočtu dáno jako
![]()
a fáze mezi výstupním a vstupním napětím v závislosti na kmitočtu je
![]() .
.
Frekvenční charakteristika je uvedena na obr. 5.17.
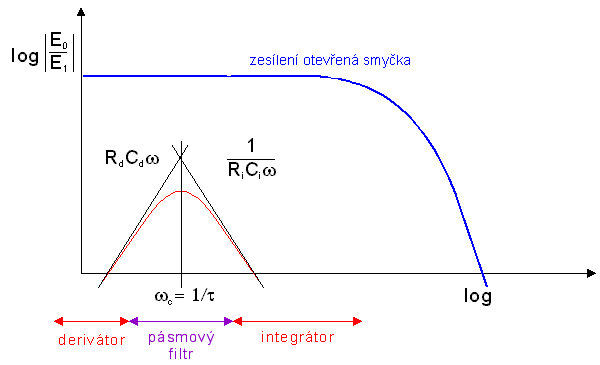
obr. 5.17
Omezení charakteristiky na vyšších frekvencích způsobí ovšem chybu z hlediska obvodu uvažovaného jako analogový derivátor. V následující tabulce jsou uvedeny chyby amplitudy a fáze výstupního napětí obvodu uvedeného na obr. 5.16 vzhledem k derivační charakteristice dané vztahem (5.3.31).
| kmitočet | 0,01 / T | 0.1 / T | 1 / T | 10 / T | 100 / T |
| rozdíl amplitud [ % ] | - 0,01 | - 0,99 | - 50 | - 99 | - 99,99 |
| rozdíl fáze | - 1,14° | - 11,42° | - 90° | - 168,57° | - 178,85° |
To znamená, že obvod uvedený na obr. 5.16 pracuje s přijatelnou chybou jako derivační obvod pouze v omezeném rozsahu frekvencí w < (0.1/t ). Pro frekvence v pásmu w > (10/t ) pracuje prakticky jako integrační.