5.3.1. Analogová integrace

Režim počátečních podmínek	Režim integrace	Režim analogové paměti

Výstupní napětí integračního obvodu je úměrné časovému integrálu vstupního napětí tj.:

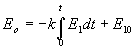(5.10)

kde E₁₀ je počáteční podmínka.

Se základním analogovým integračním obvodem jsme se setkali již v předešlé kapitole, kde je uveden na obr. 5.2b. V praxi je obvykle integrační obvod propojen tak, aby bylo možno zvolit tři pracovní režimy integračního obvodu. (Principiální zapojení je na obr. 5.12)

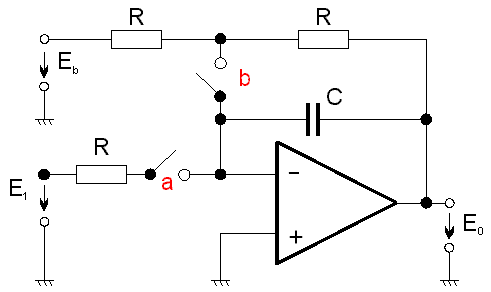
obr. 5.12

2. Režim integrace (sepnutý kontakt b , rozepnutý kontakt a ).

3. Režim paměti (režim při rozepnutém kontaktu a i b ).

V následujícím si probereme postupně všechny pracovní režimy integrátoru.

1.1. Režim počátečních podmínek

Pomocí tohoto režimu zavádíme počáteční podmínky před započetím integrace. Při sepnutém kontaktu a a rozepnutém kontaktu b platí pro operátor výstupního napětí vztah:

který si můžeme upravit na tvar:

kde a .

Průběh výstupního napětí E_o po sepnutí kontaktu a , je uveden na obr. 5.13. Po určité době, prakticky za dobu t ~ 10 t , dosáhne v tomto režimu výstupní napětí hodnoty:

,

která určuje počáteční podmínku před započetím integrace.

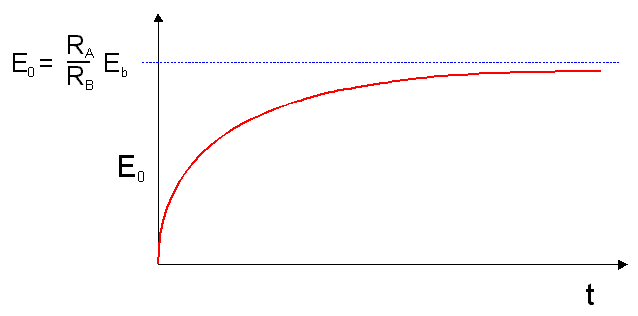
obr. 5.13

1.2. Režim integrace

Při sepnutém kontaktu b a rozepnutém kontaktu a je výstupní napětí v čase t podle vztahu (5.10) rovno:

,

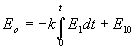kde k = 1/RC

přičemž hodnota t = 0 se přiřazuje okamžiku sepnutí kontaktu b a rozepnutí kontaktu a.

1.3. Režim analogové paměti

V režimu paměti jsou kontakty a  i   b rozpojeny a kondenzátor se vybíjí přes vstupní a výstupní odpor zesilovač; zároveň se však nabíjí výstupním napětím generovaným průchodem vybíjecího proudu vstupním obvodem zesilovače. Schematicky je situace znázorněna na obr. 5.14.

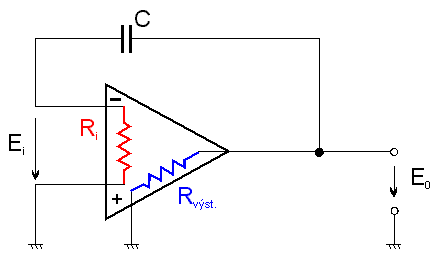
obr. 5.14

Z Kirchhofových zákonů je pro obvod na obr. 5.14 napsán vztah:

kde I_c je proud kondenzátorem. Dosazením za

E₀ = -E_iA,

kde A je zesílení operačního zesilovače, obdržíme:

,

a protože

E_i = I_cR_i ,

je ,

což je rovnice vybíjení kondenzátoru o kapacitě C přes odpor R_i(1+A) tak, že časová konstanta vybíjení je:

t = R_i(1+A)C,

Jestliže uvažujeme například R_i = 1MW, C = 1mF, A = 10⁸, je časová konstanta vybíjení analogové paměti t ~ 10⁸ s, zatímco při prostém vybíjení kondenzátoru o kapacitě C = l m F přes odpor R = 1MW je časová konstanta t = 1 s.

Analogová derivace