Proč některé látky vedou elektrický proud a jiné ne

Jak je možné, že některé látky vedou výborně elektrický proud, zatímco jiné, jinak podobných fyzikálních vlastností, jsou prakticky dokonalé izolanty?

Elektrický potenciál

Elektrický potenciál ¤ v bodě x je roven podílu práce, která se vykoná při přenesení náboje q z místa s nulovým potenciálem do místa x, a tohoto náboje.

V okolí bodového náboje ubývá elektrický potenciál se vzdáleností jako konst./r, viz obr. 1.

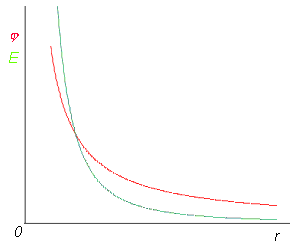
obr. 1: Velikost intenzity elektrického pole E a el. potenciál j kolem bodového náboje umístěného v bodě 0.

"Strmost" potenciálu určuje intenzitu elektrického pole a tím i sílu působící na náboj v daném místě.

V okolí atomového jádra vypadá potenciál poněkud odlišně - viz obr. 2.

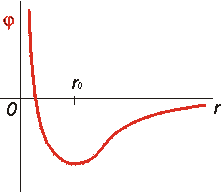
obr. 2: Elektrický potenciál j v okolí jádra atomu

Proč je potenciál jiný? Nachází-li se elektron ve vzdálenosti r>r₀ od jádra atomu, působí na něj elektrická přitažlivá síla kladného jádra. Ve vzdálenostech r<r₀ však převáží odpudivá jaderná síla, která je velmi silná. Přímo v bodě r₀ je výsledná síla působící na elektron nulová (jaderná a elektrická síla jsou zde stejně velké) a potenciál zde má minimum (a potenciální energie tedy také). Proto se elektron v atomu obvykle nachází v blízkosti této polohy (v jakési "energetické jámě"). (Ve fyzice v podstatě obecně platí princip minimální energie, tj. fakt, že soustava se v rovnovážném stavu uspořádá tak, aby její celková energie byla nejmenší možná.)

Máme-li vedle sebe (na úsečce) více atomů, vypadá celkový potenciál tak, jak je naznačeno na obrázku 3. Potenciály od jednotlivých jader se skládají, elektrony se nacházejí v prohlubních.

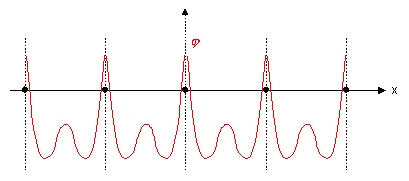
obr. 3: Průběh potenciálu podél řady atomových jader

Pauliho princip

Elektrony se v atomu nevyskytují náhodně, ale pouze v jistých stavech. Tyto stavy jsou charakterizovány čtyřmi tzv. kvantovými čísly.

Pro elektrony platí Pauliho princip: Žádné dva elektrony v atomu se nemohou nacházet ve stejném stavu (tj. nemohou mít stejná všechna čtyři kvantová čísla). Princip formuloval Wolfgang Pauli ¤.

Z tohoto principu plyne obsazení energetických hladin v atomu. V atomu jsou energetické slupky (označené K, L, M, ...). Energetické slupky jsou dány hlavním kvantovým číslem n (slupka K má n=1, slupka L má n=2 atd.). Každá slupka obsahuje podslupky (označené s, p, d, f, ...). Podslupky jsou dány vedlejším kvantovým číslem l (podslupka s má l=0, podslupka p má l=1 atd.). Slupka může obsahovat tolik podslupek, kolik l může být k příslušnému n. Například slupka K (n=1) obsahuje pouze podslupku s (l=0), slupka L (n=2) může obsahovat podslupku s (l=0) a p (l=1) atd. Možný počet elektronů v jednotlivých podslupkách ukazuje následující tabulka 2.

podslupka	možný počet elektronů	kvantové číslo l	kvantové číslo m	kvantové číslo s
s	2	0	0	±1/2
p	6	1	-1	±1/2
			0	±1/2
			1	±1/2
d	10	2	-2	±1/2
			-1	±1/2
			0	±1/2
			1	±1/2
			2	±1/2
f	14	3	-3	±1/2
			-2	±1/2
			-1	±1/2
			0	±1/2
			1	±1/2
			2	±1/2
			3	±1/2

Tabulka 2: Maximální počet elektronů v jednotlivých energetických stavech atomu

Má-li tedy například atom uhlíku elektronovou konfiguraci 1s²2s²2p² (obr. 4), znamená to, že má ve slupce K 2 elektrony (v podslupce s) a ve slupce L 4 elektrony (2 v podslupce s a 2 v podslupce p). Elektrony obsazují v základním stavu energetické hladiny od nejnižších kvantových čísel k vyšším.

Máme-li atomy daleko od sebe, jsou elektrony na svých určitých diskrétních energetických hladinách (obr. 4). Přibližujeme-li atomy k sobě, hladiny se "rozmazávají" (aby byl splněn Pauliho princip), tak aby každý elektron měl energii trochu odlišnou od ostatních. Energetické hladiny už tak nejsou diskrétní, ale pásové (přesněji řečeno - stále jsou diskrétní, ale v jistých intervalech jsou velmi blízko u sebe a v jiných nejsou žádné). Vznikají tak energetické pásy (viz. obr. 5).

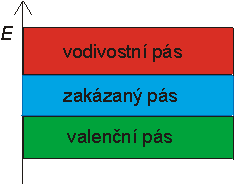
obr. 5: Schéma energetických pásů v látce

Nejzajímavější z hlediska vedení proudu jsou nejvyšší tři pásy (zobrazené na obr. 5). Čím jsou tyto pásy tak významné?
Valenční pás je poslední (nejvyšší) pás, ve kterém se v základním stavu vyskytují nějaké elektrony.
Zakázaný pás je interval energií, které nemohou elektrony nabývat (nejsou v něm žádné energetické hladiny).
Vodivostní pás je interval energií, které umožňují elektronům pohybovat se prakticky volně mezi atomy (elektrony mají tak vysokou energii, že už nejsou vázány ke konkrétním jádrům). Elektrony ve vodivostním pásu se nazývají volné a jsou to ty elektrony, které jsou nutné pro vedení proudu.

Máme-li elektron ve valenčním pásu a dodáme-li mu energii větší, než je šířka zakázaného pásu, může přejít do vodivostního pásu a přispívat k vedení proudu.

Vodivost různých látek

Z hlediska elektrické vodivosti se látky rozdělují na tři skupiny: vodiče, nevodiče a polovodiče.

Vodiče
Nemají zakázaný pás. Valenční a vodivostní pás tudíž splývají dohromady a elektrony v nich obsažené jsou prakticky volné. Je jich proto velké množství a vodiče tedy dobře vedou elektrický proud. O mechanismu vedení el. proudu v kovech se můžete dozvědět zde ¤.

Polovodiče
Obvykle mají při nulové teplotě zcela zaplněný valenční pás. Šířka zakázaného pásu je kolem 1 eV. Je tedy možno elektronům ve valenčním pásu dodat energii (teplem, světlem, elektrickým polem) a elektron se může dostat do vodivostního pásu a vést proud.

Izolanty
Mají široký zakázaný pás (přes 3 eV). Pravděpodobnost, že se do něj dostane elektron z valenčního pásu je tedy malá. Nevedou proto elektrický proud.

kvantové číslo	co určuje	jakých hodnot nabývá
n (hlavní kv. č.)	energii a velikost orbitalu ("oběžné dráhy")	0,1,2,3,...
l (vedlejší kv. č.)	moment hybnosti (tj. tvar orbitalu)	0,1,...,n-1 (pro konkrétní n)
m (magnetické kv. č.)	průmět momentu hybnosti do libovolné osy (tj. orientaci orbitu v prostoru)	-l, -l+1,..., l-1, l (pro konkrétní l)
s (spinové kv. č.)	spin (vlastní magnetický moment elektronu	-1/2, 1/2