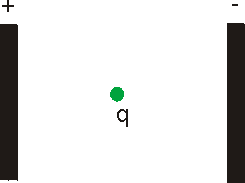
obr. 1: Náboj v homogenním elektrickém poli
Elektrostatika: El. náboj, el. síla El. pole El. potenciál a napětí Rozložení náboje na vodiči Vodič a izolant v el. poli Kapacita, kondenzátor
Mějme homogenní elektrické pole mezi dvěma nabitými deskami. Vložme
do tohoto elektrického pole náboj q.
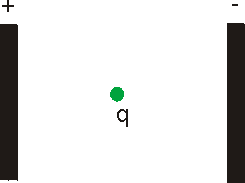
obr. 1: Náboj v homogenním elektrickém poli
Na náboj v elektrickém poli působí elektrická síla ¤
o velikosti ![]() . Síla způsobí
přemístění náboje. Bude-li náboj kladný, síla působí ve směru
elektrického pole a náboj se posouvá směrem k záporně nabité desce
("kladný náboj a záporná deska se přitahují").
. Síla způsobí
přemístění náboje. Bude-li náboj kladný, síla působí ve směru
elektrického pole a náboj se posouvá směrem k záporně nabité desce
("kladný náboj a záporná deska se přitahují").
Bude-li náboj záporný, síla působí ve směru opačném než je směr elektrického pole a náboj se posune směrem ke kladné desce.
Jaká práce se vykoná při přemístění náboje q o vzdálenost d
ve směru rovnoběžném s elektrickým polem(viz obr. 2)?
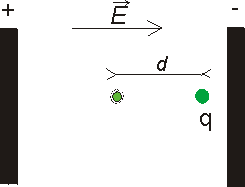
obr. 2: Práce při přemístění náboje v elektrickém poli
Práce W je obecně definována jako W=Fd, kde F je velikost síly působící na těleso (náboj) a d je dráha. Za velikost síly můžeme dosadit z definice intenzity elektrického pole F=Eq a dostaneme W=Eqd. Vykonaná práce je tedy přímo úměrná velikosti náboje. Konstantou úměrnosti je součin Ed, který je naší novou fyzikální veličinou a nazývá se elektrické napětí, značka U.
U=Ed
Co výše uvedený vztah znamená? Elektrické napětí mezi dvěma body v elektrickém poli je rovno součinu velikosti intenzity elektrického pole a vzdálenosti bodů ve směru elektrického pole.
Zavedením elektrického napětí je vztah pro práci
W = qU
Z tohoto vztahu vyplývá i další jednotka práce (a tedy i energie) - 1 elektronvolt ¤.
Práce vykonaná při přemístění náboje v elektrickém poli z bodu A do bodu B nezávisí na konkrétní dráze, po které náboj přemísťujeme. Tedy nezávisí na tom, zda jdu přímo nebo oklikou. Ověřte si to výpočtem na příkladu, který najdete zde ¤.
Jednotkou napětí je volt (V) - pojmenován po Alessandro Voltovi ¤, z výše uvedeného vztahu vyplývá 1 V=1 JC-1.

obr. 3: Různé druhy demonstračních ampérmetrů a voltmetrů (plná velikost
obrázku ¤)
 |
 |
| obr. 4: Ampérmetr/voltmetr/ohmmetr ruské výroby M4313 (plná velikost obrázku ¤, plná velikost s popisky ¤) | obr. 5: Ampérmetr/voltmetr/ohmmetr HC-2030ET (plná velikost obrázku ¤, plná velikost s popisky ¤) |
 |
|
| obr. 6: Ampérmetr/voltmetr/ohmmetr M890C+ (plná velikost obrázku ¤, plná velikost s popisky ¤) | |
Zapojení voltmetru - paralelně k objektu, na kterém chceme měřit napětí ("vedle něho") (obr. 7).
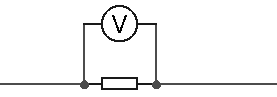
obr. 7: Připojení voltmetru k měřenému objektu (zde rezistoru)
O principu funkce klasického voltmetru a změně jeho rozsahu si přečtěte zde ¤.
Spočtěte si úlohy ¤.
Již zde byla jednou zmíněna jistá podobnost elektrického pole s gravitačním polem. Máme-li například míč v gravitačním poli, má jistou potenciální energii. Zvedneme-li míč výše, tj. pohybujeme-li s ním proti směru gravitační síly, jeho potenciální energie se zvětšuje, necháme-li ho spadnout níže (pohybuje se ve směru gravitační síly), jeho potenciální energie se zmenšuje.
Podobně je tomu v elektrickém poli. Pohybuje-li se náboj proti směru
elektrické síly, zvyšuje se jeho elektrická potenciální
energie,
pohybuje-li se ve směru síly, jeho elektrická potenciální energie se
zmenšuje.
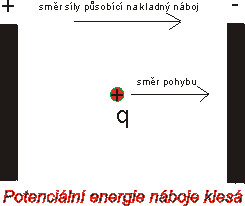 |
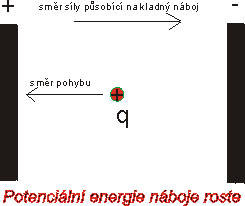 |
|
obr.8, 9: Potenciální energie náboje v elektrickém poli |
|
Proč tomu tak je? Energie je schopnost konat práci. Čím větší energii částice s nábojem má, tím větší práci může vykonat. Bude-li na obrázku výše kladně nabitá částice u kladně nabité desky, bude urychlována elektrickou silou směrem k záporně nabité desce (přitom se její elektrická potenciální energie bude měnit na energii kinetickou) a při srážce s nějakým atomem ho může například uvést do pohybu a tak konat práci.
Změna energie DEp při přemístění částice z místa A do místa B je obecně rovna práci W (dodané nebo vykonané), DEp=W.
Vyjádříme práci pomocí elektrického napětí a náboje a vypočteme napětí:
W=qU
qU=DEp=EpA-EpB
![]()
Definujeme novou fyzikální veličinu, elektrický potenciál j, vztahem
j =Ep/q.
Elektrický potenciál v daném místě pole je roven podílu elektrické
potenciální energie Ep bodového náboje q v tomto místě
elektrického pole a tohoto náboje q.
Potenciál Země a uzemněných těles definujeme rovný nule.
Elektrický potenciál v bodě x je tedy roven podílu práce, kterou je
třeba vykonat na přenesení náboje z uzemněného tělesa do bodu x, a
velikosti tohoto náboje.
Pomocí potenciálu můžeme zapsat elektrické napětí jako
UAB = jA - jB
Napětí mezi body A a B je rovno rozdílu potenciálů v těchto bodech. Každému místu v elektrickém poli přísluší nějaký potenciál. Mezi dvěma místy s rozdílným potenciálem je elektrické napětí.
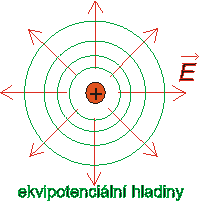
Místa v elektrickém poli, která mají stejný potenciál, se nazývají ekvipotenciální hladiny. Mezi dvěma body, které leží na stejné ekvipotenciální hladině, je nulové elektrické napětí.
 |
 |
|
obr. 10: Ekvipotenciální hladiny v radiálním elektrickém poli (intenzita el. pole je v různých bodech různá co do velikosti i co do směru) |
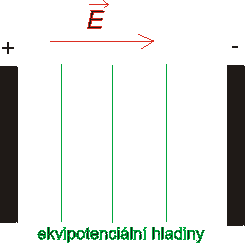
obr. 11: Ekvipotenciální hladiny v homogenním elektrickém poli (intenzita el. pole je všude stejná co do velikosti i co do směru) |
Zbývá otázka, co nám říká samotný potenciál. Jaký je průběh potenciálu v okolí nabitých těles? Vypočtěte si následující úlohy ¤.
Další kapitola: Jak oddělit kladný a záporný náboj od sebe? ¤