
- Jak je možné, že nabité těleso může přitahovat těleso nenabité?
- Jak fungují elektrostatické filtry kouřových plynů?
- Čím je napájen blesk u fotoaparátu?
Elektrostatika: El. náboj, el. síla El. pole El. potenciál a napětí Rozložení náboje na vodiči Vodič a izolant v el. poli Kapacita, kondenzátor
 |
|
Na izolovaném nabitém vodiči je náboj rozložen vždy na jeho vnějším povrchu (obr. 1) a to tak, aby náboje byly v rovnováze. Zavádí se plošná hustota náboje s na povrchu tělesa vztahem
![]()
kde DS je obsah plochy a DQ náboj na této ploše. Plošná hustota náboje je největší v těch místech vodiče, která jsou nejvíce zakřivena směrem ven (hrany, hroty), nejmenší je v dutinách.
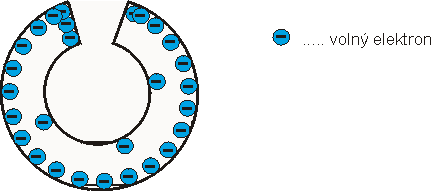
obr. 1: Záporně nabité izolované vodivé těleso
V okolí nabitého vodiče vzniká elektrické pole. V okolí koule nabité nábojem Q je elektrické pole stejné jako v okolí bodového náboje Q, který by byl v místě středu koule. Na povrchu koule poloměru R ve vakuu je tedy intenzita elektrického pole
![]()
Uvnitř koule je intenzita el. pole nulová (jinak by jí tekl el. proud). Jelikož pro povrch S koule platí vztah S = 4pR2, máme po dosazení do předchozího vztahu
![]()
a vzhledem k definici plošné hustoty náboje ¤ s je nakonec
![]()
Tento vztah platí i pro intenzitu el. pole u povrchu nabitého vodiče jiného než kulového tvaru ve vakuu. Je-li vodič v prostředí o permitivitě e, platí
![]()
Ze vztahu vyplývá, že el. pole je nejsilnější tam,
kde je největší hustota náboje, tedy u hrotů a hran.
Kde to můžeme vidět?
Elektrický vítr, sršení náboje.
Má-li těleso dostatečně ostrý hrot, může se i při malých hodnotách potenciálu tělesa vytvořit v okolí hrotu "elektrický vítr". Elektrické pole v blízkosti hrotu je totiž tak silné, že ionizuje molekuly vzduchu. Ty ionty, které mají náboj stejné polarity jako je náboj hrotu, jsou od hrotu odpuzovány. Přitom s sebou strhují i okolní molekuly vzduchy a vzniká vítr. Opačně nabité ionty se k hrotu přibližují a neutralizují ho.
Tento jev (zde nazývaný sršení náboje) také způsobuje ztráty ve vedení vysokého napětí - viz výboje v plynech ¤..
Elektrostatické filtry
| Elektrostatický filtr (odlučovač) se používá například v elektrárnách na zachycování popílku vyletujícího z komína. Částečky popílku se z napnutého drátu s potenciálem až -100 kV záporně nabijí. Proto jsou pak od drátu odpuzovány a hromadí se tak na uzemněných stěnách filtru a vlastní vahou se sesouvají do jeho spodní části, odkud jsou čas od času odstraňovány (obr. 2). | 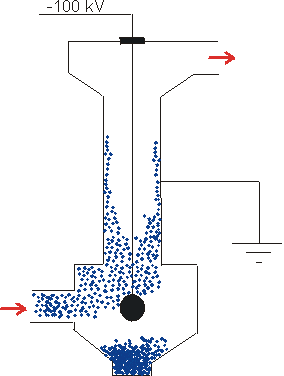 obr. 2: Elektrostatické odlučování popílku |
Vložíme vodič do elektrického pole mezi dvěma nabitými deskami (obr. 3). Co se stane s nábojem ve vodiči?
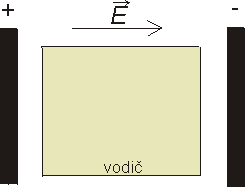
obr. 3: Vodič v homogenním elektrickém poli
Volné elektrony ve vodiči budou přitahovány kladnou deskou a přemístí se tedy proti směru elektrického pole => levá část vodiče se nabije záporně. A protože se volné elektrony přemístily doleva, je vpravo přebytek kladného náboje => pravá část vodiče je nabitá kladně (obr. 4). Tento jev se nazývá elektrostatická indukce. Elektrické pole mezi deskou a krajem vodiče (na obou stranách) je stejné jako původně, uvnitř vodiče je intenzita elektrického pole nulová. Kdybychom teď vodič rozdělili na dva kusy, bude jeden z nich nabitý záporně a druhý kladně.
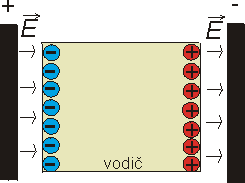
obr. 4: Elektrostatická indukce
Proč je intenzita elektrického pole ve vodiči nulová?
Izolanty (dielektrika) neosahují volné elektrony, proto u nich nemůže nastávat elektrostatická indukce.
Dělí se na dva druhy:
1. Polární dielektrika (např. voda) -
jejich molekuly mají střed ("těžiště") kladného náboje jinde
než střed záporného náboje. Při vložení látky do elektrického pole se
molekuly natočí tak, aby jejich "kladnější" konec směřoval k záporné
desce a "zápornější" konec ke kladné desce (obr. 5, 6). Jev se
nazývá polarizace dielektrika. V dielektriku se
tak vytvoří vnitřní el. pole (podobně jako tomu bylo ve vodiči), které má
opačný směr než pole vnější, ale jeho intenzita je menší. Výsledné
elektrické pole v dielektriku má tedy směr stejný jako vnější pole a je o
něco menší. Poměr velikostí vnějšího el. pole E1 a výsledného
pole v dielektriku E je relativní permitivita er
dielektrika ¤, ![]() .
Relativní permitivita prostředí je tedy vždy větší než jedna.
.
Relativní permitivita prostředí je tedy vždy větší než jedna.
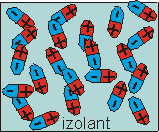 obr. 5: polární dielektrikum bez přítomnosti el. pole |
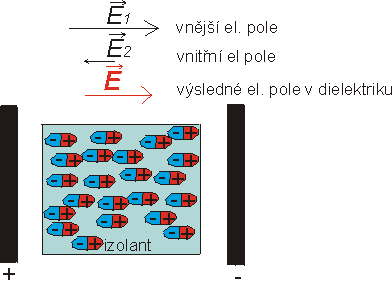 obr. 6 Polární dielektrikum v elektrickém poli |
2. Nepolární dielektrika - jejich molekuly mají střed kladného náboje na stejném místě jako střed záporného náboje (molekula může např. vypadat jako koule). Při vložení látky do elektrického pole je však kladný náboj molekuly přitahován na jednu stranu a záporný náboj na druhou stranu a molekula se "protáhne" ve směru el. pole (obr. 7). Tím se střed kladného náboje dostane jinam než střed záporného náboje a situace vypadá obdobně jako na obr. 6. Jak už bylo řečeno, jev se nazývá polarizace dielektrika. O elektrickém poli uvnitř dielektrika a relativní permitivitě platí totéž jako u polárního dielektrika ¤.
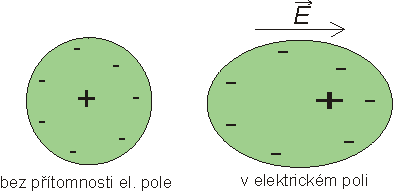
obr. 7: Molekula nepolárního dielektrika bez el. pole a její polarizace
Ozdoby v pokoji - brčka na zdi ¤
Připojíme-li izolovaný vodič ke svorce zdroje napětí, bude mít stejný potenciál j jako svorka. Náboj Q, který na něj ze svorky přiteče, je přímo úměrný tomuto potenciálu,
Q = C.j,
kde C je konstanta úměrnosti. Pro daný vodič je to konstanta, která závisí na tvaru a velikosti vodiče, a nazývá se kapacita vodiče, jednotka 1 F (farad). Jednotka byla pojmenována po Michaelu Faradaym ¤. Pro praktické použití je příliš velká, používají se mF, mF, nF a pF.
Elektrická součástka, která má jako svou význačnou vlastnost přesně určenou kapacitu, se nazývá kondenzátor. V nejjednodušším případě je kondenzátor tvořen dvěma rovnoběžnými deskami od sebe izolovanými dielektrikem (např. vzduchem). Připojíme-li vývody kondenzátoru ke svorkám zdroje napětí, vytvoří se na desce s vyšším potenciálem jA náboj Q a na desce s nižším potenciálem jB náboj -Q. Mezi deskami je elektrické pole o intenzitě
![]()
kde d je vzdálenost mezi deskami kondenzátoru a U napětí mezi nimi. Mezi nábojem na kondenzátoru a napětím mezi deskami platí vztah (obdobný tomuto ¤)
Q = C.U
Kapacita deskového kondenzátoru, který má plochu desek S (přesně řečeno, je to plocha, kterou se desky překrývají) a jejich vzdálenost d a je vyplněn dielektrikem s permitivitou e ¤, je
![]()
(odvození zde ¤). Čím větší je permitivita dielektrika,tím větší kapacitu kondenzátor má.
obr. 8: schematická značka kondenzátoru
Kondenzátory existují v nejrůznějších provedeních (viz obr. 9,10)
 |
 |
| obr. 9: Různé druhy kondenzátorů (odshora kondenzátory s kapacitami 100 nF (v držáku), 500 nF, 1 mF, 3,3 mF a 10 mF) | obr. 10: Otočný kondenzátor (s proměnnou účinnou plochou desek a tedy proměnnou kapacitou) z rádiového přijímače |
O označování a kapacitě vyráběných kondenzátorů se můžete dozvědět zde ¤.
Elektrické pole v kondenzátoru má také svoji energii. Na její vyjádření se můžete podívat zde ¤.
Spočítejte si úlohy ¤.
Spojování kondenzátorů
Paralelní zapojení
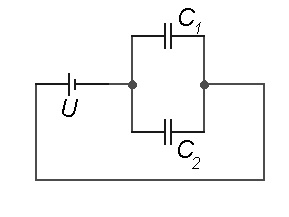
obr. 10: Paralelní zapojení kondenzátorů.
Oba dva kondenzátory se nabijí na napětí zdroje U. Na desky kondenzátoru se musí přivést celkový náboj Q, přičemž ten je součtem nábojů přivedených na jednotlivé kondenzátory, Q = Q1+Q2. Vyjádříme-li v tomto vztahu náboje pomocí napětí (která jsou na obou kondenzátorech stejná - napětí je rozdíl potenciálů mezi dvěma body) a kapacit, máme CU = C1U+C2U a po vykrácení je
C = C1+C2,
kde C je kapacita kondenzátoru, kterým můžeme nahradit kondenzátory C1 a C2, aniž by se poměry v obvodu změnily.
Sériové spojení kondenzátorů
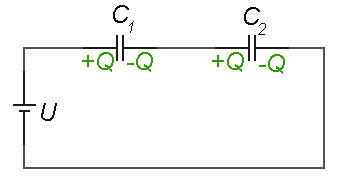
obr. 11: Sériové spojení kondenzátorů
Na krajních deskách obou kondenzátorů připojených ke zdroji napětí se
objeví náboj +Q a -Q. Na protějších deskách příslušných
kondenzátorů se elektrostatickou indukcí vytvoří náboj -Q a +Q
(obr. 9). Kondenzátory jsou zapojeny sériově, čili součet napětí na nich
je roven napětí zdroje, U = U1+U2. Vyjádříme-li
v tomto vztahu napětí pomocí nábojů a kapacit, máme ![]() a po vykrácení je
a po vykrácení je
![]() ,
,
kde C je kapacita kondenzátoru, kterým můžeme nahradit kondenzátory C1 a C2, aniž by se poměry v obvodu změnily.
Další ("velká") kapitola: Elektrický proud ¤