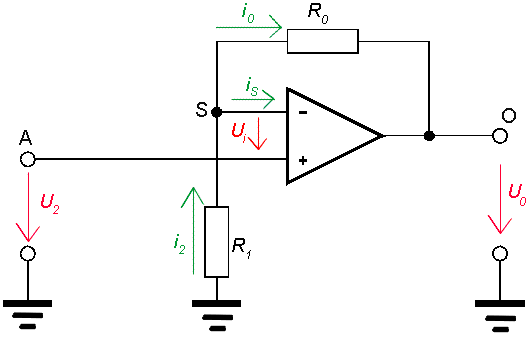
obr. 1: Operační zesilovač v zapojení s neinvertujícím vstupem
Integrované obvody: Úvod Operační zesilovač Zapojení OZ s invert. vstupem Zapojení OZ s neinvert. vstupem Sčítání a odčítání pomocí OZ Násobení a dělení pomocí OZ
Zapojení operačního zesilovače s invertujícím vstupem je na obr.1. Zapojení je opět se zpětnou vazbou, tj. přes rezistor R0 je spojen vstup a výstup zesilovače.

obr. 1: Operační zesilovač v zapojení s neinvertujícím vstupem
Opět: vstupní odpor ideálního operačního zesilovače je nekonečný, tj. mezi svorkami + a - nepoteče operačním zesilovačem žádný proud (iS = 0), tedy napětí Ui = 0.
Z Ohmova zákona můžeme vyjádřit proudy pomocí napětí a odporů.
Proud i2 je proud tekoucí odporem R1.
Je tedy roven i2 = UR1/R1,
kde UR1 je napětí na rezistoru R1. To je
rovno rozdílu potenciálů
¤ mezi zemí a bodem S. Potenciál země je nulový, potenciál jS
v bodě S je roven U2 + Ui. Ale Ui = 0,
tedy potenciál v bodě S je roven U2.
Tedy UR1 = 0 - jS = -U2
a proud ![]() .
.
Proud i0 je proud tekoucí odporem R0.
Je tedy roven i0 = UR0/R0,
kde UR0 je napětí na rezistoru R0. To je
rovno rozdílu potenciálů
¤ mezi body S a O. Potenciál jS
v bodě S je roven U2. Potenciál jO
v bodě O je roven U0, protože U0
je napětí mezi tímto bodem a zemí.
Tedy UR0 = jS - jO = U2 - U0 a
proud ![]() .
.
Proud iS je roven nule (viz výše ¤).
Mezi proudy iS, i1 a i0 můžeme napsat následující vztah (1. Kirchhoffův zákon pro bod S): iS + i0 = i2. Protože iS = 0, platí i2 = i0. Po dosazení z Ohmova zákona dostáváme vztah pro výstupní napětí U0
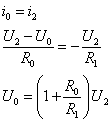
Zesílení zesilovače je v tomto zapojení opět určeno podílem odporů použitých rezistorů. Výstupní napětí má stejnou fázi jako vstupní napětí (obr. 2).

obr. 2: Příklad průběhů napětí na vstupu (U2) a výstupu
(U0) operačního zesilovače zapojeného s neinvertujícím
vstupem. Napětí mají stejnou fázi, poměr odporů rezistorů (tj. zesílení
zesilovače v tomto zapojení) je 3.
Další kapitola: Použití operačního zesilovače pro základní aritmetické operace ¤