 |
Hodnoty odporů a napětí:
U1=10 V R1=10 W |
Ohmův zákon: Základní pokus Výsledky pokusu Ohmův zákon Rezistor, reostat, potenciometr Spojování rezistorů Ohmův zákon pro uzavřený obvod Kirchhoffovy zákony
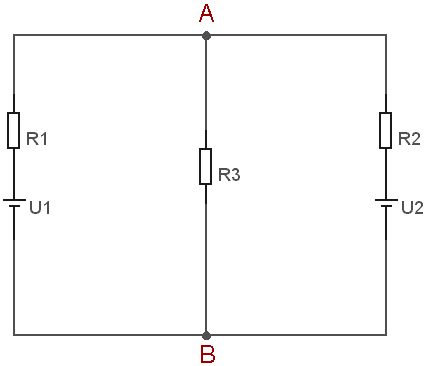
Máme-li nějaký elektrický obvod s rezistory (cívkami, kondenzátory apod.)(např. tento) a známe-li napětí použitých zdrojů a parametry součástek (např. odpory rezistorů), zajímají nás obvykle proudy tekoucí větvemi obvodu a napětí na součástkách.
Na výpočet je možno použít Ohmův zákon, dále se používají dva Kirchhoffovy zákony.
Názvosloví:
UZEL - místo v obvodu, kde se vodivě stýkají nejméně tři vodiče (na příkladu
to jsou body A a B)
VĚTEV - část obvodu mezi dvěma uzly - všemi prvky v jedné větvi protéká
stejný proud (na příkladu to jsou všechny úseky mezi
body A, B)
1. Kirchhoffův zákon: Součet všech proudů přitékajících do uzlu je v každém okamžiku roven nule. Proudy tekoucí do uzlu bereme se záporným znaménkem a proudy vytékající z uzlu s kladným znaménkem.
Zapsáno rovnicí: I1+I2+I3+...=0
2. Kirchhoffův zákon: Součet napětí na všech prvcích (aktivních (zdrojů) i pasivních (rezistorů,...)) podél uzavřené smyčky je v každém okamžiku roven nule. Přitom napětí na rezistorech vyjadřujeme jako U=RI, kde R je odpor rezistoru a I proud jím protékající. Je-li smyčka orientována souhlasně se šipkou značící směr proudu nebo polaritu zdroje (zde šipka směřuje od + pólu k - pólu), bereme příslušný člen s kladným znaménkem, v opačném případě se záporným znaménkem.
Zapsáno rovnicí U1+U2+U3+...=0
Volba směru šipek na začátku je libovolná, potom se však už musí dodržovat.
Máme elektrický obvod se dvěma bateriemi a třemi rezistory (obr. 1). Vypočtěte proudy tekoucí jednotlivými větvemi a napětí na jednotlivých rezistorech.
 |
Hodnoty odporů a napětí:
U1=10 V R1=10 W |
1. Označíme si v obrázku šipky u zdrojů napětí (od "+ k -") a vyznačíme libovolně směry proudu v jednotlivých větvích. Dále si zvolíme uzavřené smyčky (stačí jich tolik, kolik "okének" je ve schématu, v tomto případě tedy dvě).
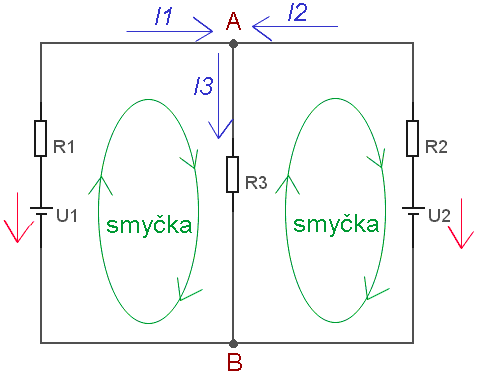 |
Smyčka vlevo má stejnou orientaci jako proudy procházející
rezistory R1a R3 a opačnou než napětí
zdroje U1.
Smyčka vpravo má opačnou orientaci než proudy procházející rezistory R2a R3 a stejnou jako napětí zdroje U2. |
2. Napíšeme první Kirchhoffův zákon např. pro uzel A: Proudy I1 a I2 vtékají do uzlu (tedy kladné znaménko), proud I3 z uzlu vytéká (tedy záporné znaménko).
I1+I2 - I3 = 0
3. Napíšeme druhý Kirchhoffův zákon pro obě smyčky:
levá smyčka: R1I1+R3I3 - U1 = 0
pravá smyčka: -R2I2 - R3I3 + U2 = 0
4. Máme teď tři rovnice pro tři proudy I1, I2, I3:
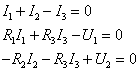
Tyto rovnice vyřešíme. Jelikož obecné řešení je komplikované, zavedeme místo I1, I2, I3 proměnné i1, i2, i3 označující číselné hodnoty proudů (v ampérech) a za odpory a napětí dosadíme jejich číselné hodnoty (v základních jednotkách, tj. ohmech, resp. voltech).
Máme rovnice 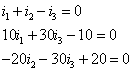
Ty vyřešíme. Výsledkem jsou čísla i1 = -1/11,
i2 = 5/11, i3 = 4/11, tedy
proudy
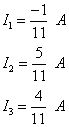
Proud I1 vyšel se záporným znaménkem. Znamená to, že jeho skutečný směr je opačný než směr námi zvolený. U ostatních proudů souhlasí zvolené směry se skutečnými.
Napětí na jednotlivých rezistorech se spočte z Ohmova zákona.
Další úlohy jsou ve sbírce příkladů, kapitola 1 ¤ a na této stránce ¤..
Zkuste si pohrát též s následujícími Java aplety:
| Kirchhoffovy zákony - obvod 1 ¤ |
| Kirchhoffovy zákony - obvod 2 ¤ |
| Kirchhoffovy zákony - obvod 3 ¤ |
| Kirchhoffovy zákony - obvod 4 ¤ |
| Kirchhoffovy zákony - obvod 5 ¤ |
Další ("velká") kapitola: Polovodiče ¤