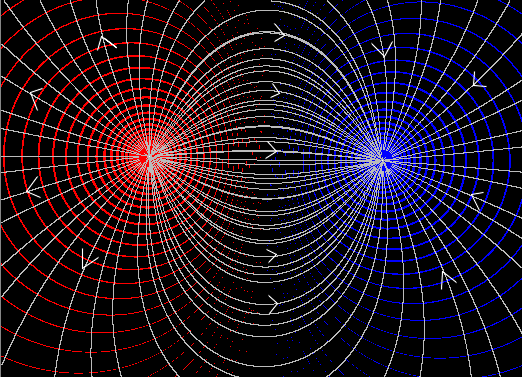
(směr je zakreslen jen u některých siločar)
Písemné práce: Test 1 (2.10.03) Test 2 (30.10.03) Test 3 (15.12.03) Test 4 (8.1.04) Test 5 (4.2.04) Test 6 (1.4.04)
Jaký je náboj olejové kapičky o hmotnosti 1.10-16 kg, která se vznáší v laboratoři v elektrickém poli, jehož intenzita má směr vzhůru a má velikost 1225 Vm-1. Výsledek vyjádřete v jednotkách elementárního náboje e. Napište též, zda je náboj kapky kladný či záporný.
| m = 1.10-15 kg E = q = ? |
Jelikož se kapka vznáší, je velikost tíhové síly na ni působící
rovna velikosti síly elektrické
Fe = FG Elementární náboj e = 1,6.10-19 C, tedy náboj kapky q = 8.10-19/1,6.10-19 e = 5e. Aby elektrická síla kompenzovala tíhovou, musí elektrická síla působit směrem vzhůru, tedy stejným směrem jako je směr intenzity elektrického pole a náboj kapky je tudíž kladný. Kapka má kladný náboj o velikosti pětinásobku elementárního náboje. |
Příslušné učivo k této úloze je zde.
Desky kondenzátoru jsou od sebe vzdáleny 10 cm. Pravá deska je na potenciálu 10 kV, levá deska je uzemněna (má potenciál 0 V). Jaký je potenciál uvnitř kondenzátoru v místě vzdáleném 3 cm od pravé desky?
Jelikož je levá deska na potenciálu 0 V, bude potenciál v bodě vzdáleném 3 cm od pravé (a tedy 7 cm od levé) desky roven napětí mezi tímto bodem a levou deskou.
| U = 10 kV l = 10 cm d = 7 cm |
Mezi deskami je homogenní el. pole o intenzitě velikosti
E = U/l. Napětí Ud mezi
levou deskou a bodem ve vzdálenosti d od ní je Ud = Ed = Ud/l = 10.7/10 kV = 7 kV.
V dotyčném místě je elektrický potenciál 7 kV. |
Příslušné učivo k této úloze je zde.
Nakreslete průběh siločar el. pole a ekvipotenciálních ploch v okolí dvojice nábojů (jeden kladný, druhý záporný). Zdůvodněte, proč jsou siločáry kolmé k ekvipotenciálním plochám.

(směr je zakreslen jen u některých siločar)
Pohybuje-li se náboj po ekvipotenciální ploše, má stále stejnou potenciální energii a tudíž elektrické pole na něm nekoná práci. Práce je dána jako W = F.s.cosa, kde F je síla působící na částici, s je její dráha a a je úhel, která svírá směr síly (ten je dán tečnou k siločáře) se směrem dráhy (ta je dána ekvipotenciální plochou). Práce se nekoná je-li tento úhel pravý.
Příslušné učivo k této úloze je zde.