 |
 |
Zápisy do sešitu: El. náboj a síla Elektrické pole Práce v el. poli Rozložení náboje na vodiči Vodič v el. poli Izolant v el. poli Kapacita, kondenzátor El. proud Vodiče, polovodiče, nevodiče Prakt. práce: měření VA char. rezistoru Ohmův zákon Rezistor, reostat, potenciometr Spojování rezistorů Ohmův zákon pro celý obvod Kirchhoffovy zákony Vlastní polovodič Termistor Fotorezistor Dioda - pokusy Příměsový polovodič Princip diody Usměrňování diodou Graetzovo zapojení Praktické ovládání generátoru a osciloskopu Náhr. schéma diody Kondenzátor ve střídavém obvodu Kapacita diody VA char. diody a Zenerovy diody Zdvojovač napětí Televize a osciloskop Urychlování elektronů Vychylovací destičky Stacionární magnetické pole Magnetická síla (zač. a pokr.) Magn. poli přímého vodiče Mag. pole závitu a cívky Nabitá částice v mag. poli Shrnutí televize a osciloskopu Síla působící mezi dvěma vodiči Stejnosměrný elektromotor Magnetické vlastnosti materiálů Elektromagnet El. zvonek Elmag. relé Druhy elektromotorů Elmag. indukce - vznik ind. napětí Faradayův zák. elmag. ind. Magn. ind. tok Ind. proud Vířivé proudy Vl. indukce Zhášecí obvody cívek Rekuperační dioda Energie el. a mag. pole El. proud v plynech Jiskrový výboj Obloukový výboj Doutnavý výboj Koróna, katodové a kanálové záření LED Žárovka Bipolární tranzistor Unipolární tranzistor Operační zesilovač Práce a výkon Ef. hodnota proudu Regulace výkonu Tyristor Přenos rádiového signálu Amplitudová modulace Frekvenční modulace Sériový RLC obvod Fázorový diagram Elmag. oscilátor Výkon v RLC obvodu Amplitudová demodulace (krystalka) Frekvenční demodulace Rádiový přijímač Stereofonní vysílání Televize El. proud v kapalinách
57. a 58. hodina - pondělí 17.5. 2004
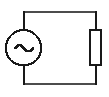
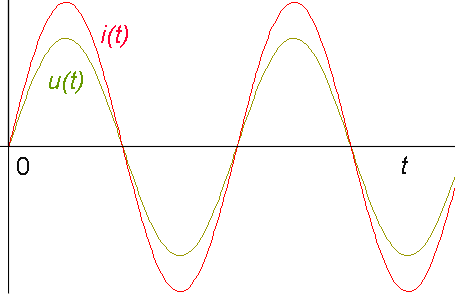
Obvodem prochází střídavý proud, jehož časový průběh je stejný jako časový průběh napětí zdroje (které je rovno napětí na rezistoru) a jehož amplituda je I0 = U0 /R, kde U0 je amplituda napětí na rezistoru.
 |
 |
Matematicky: má-li napětí časový průběh u(t) = U0 sin(w t), má proud časový průběh i(t) = I0 sin(w t) = (U0 /R)sin(w t). Odpor rezistoru R se nazývá rezistance rezistoru XR.
Kondenzátor se periodicky nabíjí a vybíjí, obvodem prochází střídavý proud.
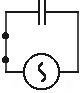 |
Kondenzátor má jistý "odpor" - kapacitance kondenzátoru XC. Je dána jako XC=1/w C (w = 2p f, kde f je frekvence střídavého proudu). Kapacitance je tím větší, čím menší je kapacita kondenzátoru a čím menší je frekvence proudu. Mezi amplitudami proudu a napětí platí vztah I0 = U0 /XC = w CU0.
Napětí na kondenzátoru a proud procházející obvodem nejsou ve fázi - proud předbíhá napětí o čtvrtinu periody. Po sepnutí spínače začne obvodem procházet proud, který nabíjí kondenzátor. Jak roste napětí na kondenzátoru, nabíjecí proud klesá. Ve chvíli, kdy je napětí největší, se změní směr proudu. Proud začíná procházet opačným směrem a zvětšuje se, kondenzátor se vybíjí a napětí na něm klesá atd.
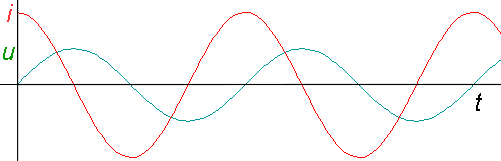
Matematicky: má-li napětí časový průběh u(t) = U0 sin(w t), má proud časový průběh i(t) = I0 sin(w t + p /2) = w CU0 sin(w t + p /2) (obr. 5).
Mějme stejnosměrný obvod s cívkou o indukčnosti L . Po sepnutí spínače se na cívce indukuje napětí, které je stejně velké jako napětí zdroje, ale má opačnou fázi. Proud obvodem je v tu chvíli nulový a začíná růst, napětí indukované na cívce se zmenšuje. Obvodem poteče maximální proud tehdy, když napětí indukované na cívce bude nulové. Proud tedy "následuje napětí".
Nyní zaměníme stejnosměrný zdroj za zdroj střídavého napětí . Děj nastává opakovaně, obvodem prochází střídavý proud. Podobně jako u kondenzátoru, proud není ve fázi s napětím na cívce, ale na rozdíl od kondenzátoru napětí předbíhá proud o čtvrtinu periody.
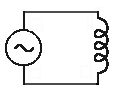 |
Cívka má také jistý "odpor" - induktance cívky XL. Je dána jako XL=w L (w = 2p f, kde f je frekvence střídavého proudu). Induktance je tím větší, čím vetší je indukčnost cívky a čím větší je frekvence proudu. Mezi amplitudami proudu a napětí platí vztah I0 = U0 /XL = U0 / w L.
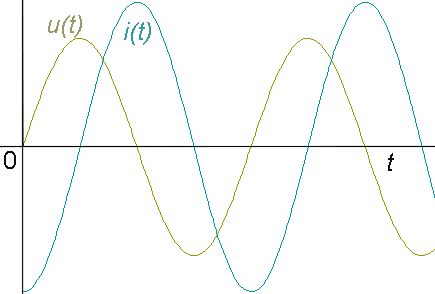
Matematicky: má-li napětí časový průběh u(t) = U0 sin(w t), má proud časový průběh i(t) = I0 sin(w t - p /2) = (U0 / w L)sin(w t - p /2).
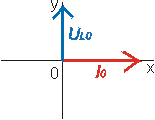
Fázor je rotující orientovaná šipka umístěná v počátku soustavy souřadné, jejíž velikost udává amplitudu veličiny a průmět konce do svislého směru (y - ová souřadnice konce fázoru) udává hodnotu veličiny v příslušném okamžiku.
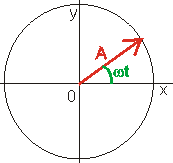
Do fázorového diagramu můžeme znázornit napětí a proud na jednotlivých prvcích střídavého obvodu. Fázor proudu se obvykle kreslí v kladném směru osy x. Fázor napětí na rezistoru se rovnoběžný s fázorem proudu, fázor napětí na cívce "předbíhá" fázor proudu o p/2 a fázor napětí na kondenzátoru se "zpožďuje" za fázorem proudu o p/2.
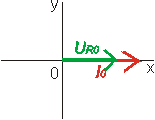 |
 |
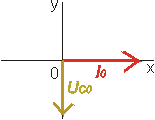 |
||
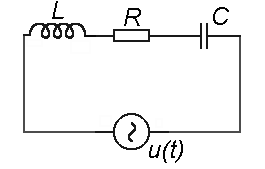
Sériový obvod se zdrojem střídavého napětí, rezistorem, cívkou a kondenzátorem - RLC obvod. Poměry v obvodu vyznačíme do fázorového diagramu. Jelikož jde o sériový obvod, protéká všemi prvky stejný proud. Na každém prvku je však jiné napětí.
 |
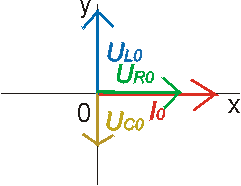 |
Jaké je celkové napětí na sériové kombinaci R, L, C? Je to "vektorový součet" jednotlivých napětí na R, L, C. Napřed od sebe odečteme UL0 a UC0 a potom výsledek vektorově složíme s UR0.
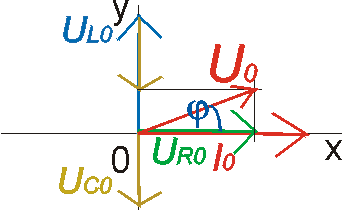
Napětí může předbíhat proud nebo se za ním zpožďovat - záleží na vzájemném poměru UL0 a UC0.
Algebraicky vypočteme výsledné napětí U0 z Pythagorovy věty:
![]() .
.
59. hodina - čtvrtek 20.5. 2004
Test na elektromagnetickou indukci a el. proud v plynech - zadání zde ¤.
Impedance RLC obvodu:
Pro jednotlivá napětí platí:
U0 = ZI0
UR0 = RI0
UL0 = XLI0 = w LI0
UC0 = XCI0 = I0/w C.
Dosadíme do vztahu pro U0: 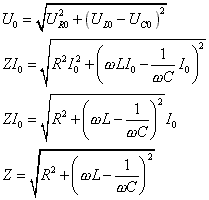
... celková impedance v sériovém zapojení
Platí 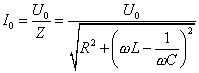
Amplituda elektrický proud tekoucího obvodem závisí nejen na amplitudě napájecího napětí, ale i na jeho frekvenci ... rezonanční křivka.
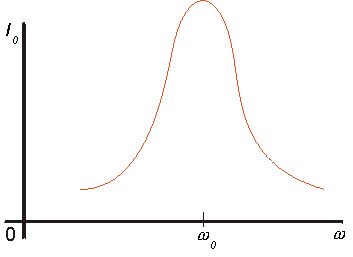
Rezonanční kruhová frekvenci w 0
... maximální proud, minimální
impedance 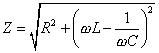 => minimální člen pod
odmocninou. První člen na frekvenci nezávisí =>
=> minimální člen pod
odmocninou. První člen na frekvenci nezávisí => ![]() musí být nulový.
musí být nulový.
V rezonanci 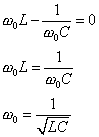
Rezonanční frekvence ![]() .
.
60. a 61. hodina - pondělí 24.5. 2004
- jednoduchý LC obvod 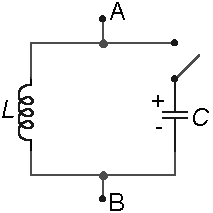
Na začátku kondenzátor nabit. Po sepnutí spínače se začíná vybíjet přes cívku. Tím se na vývodech cívky indukuje napětí, proud postupně narůstá (jako u přechodového jevu při zapnutí proudu ve stejnosměrném obvodu s cívkou ¤). Když proud obvodem dosáhne maximální hodnoty, napětí na cívce (a tedy i na kondenzátoru - jsou spojeny paralelně) je nulové. Kondenzátor je vybitý, obvodem teče proud - kondenzátor se začíná nabíjet na opačnou polaritu, proud obvodem klesá. Na cívce se indukuje napětí, které podporuje průchod proudu. V okamžiku, kdy proud ustane, je na cívce i kondenzátoru největší napětí, kondenzátor je nabit (na opačnou polaritu než předtím) a začíná se zase vybíjet (ale s opačnou polaritou). Tento děj se periodicky opakuje. Proud procházející obvodem má sinusový průběh.
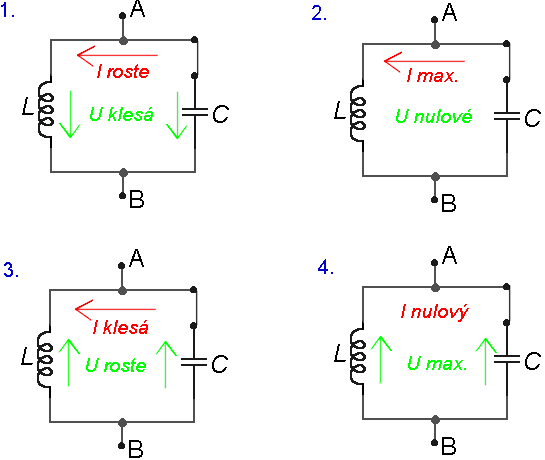
Eenergie: Na začátku je kondenzátor nabit - má energii elektrostatického pole. Tím, jak se vybíjí, se jeho energie elektrostatického pole mění na energii magnetického pole cívky. Poté, co se zcela vybije a začíná se nabíjet na opačnou polaritu, se energie magnetického pole cívky opět mění na energii elektrického pole kondenzátoru. Energie se takto periodicky předává mezi cívkou a kondenzátorem. Kdyby byly prvky ideální, žádná by se neztrácela - střídavý proud v obvodu by měl stále stejnou amplitudu.
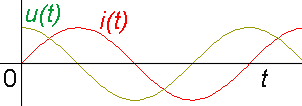
Reálné prvky ideální nejsou. Cívka nemá jen indukčnost, ale také nějaký elektrický odpor vinutí. Díky tomu se část energie přeměňuje na teplo a tak se zmenšuje amplituda proudu - obvod koná tlumené kmity.
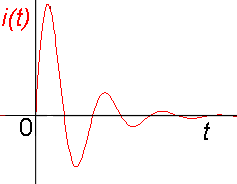
Frekvence střídavého proudu je rovna rezonanční frekvenci RLC obvodu
se stejnou cívkou a kondenzátorem - ![]() .
.
Okamžitá hodnota výkonu p(t) v obvodu s rezistorem o odporu R je p(t) = i(t)u(t) = Ri2(t) a střední hodnota výkonu je P = RIef2, kde Ief je efektivní hodnota střídavého proudu .
Na cívce "napětí předbíhá proud" o p/2,
jejich časové průběhy jsou u(t) = U0 sin(w t), i(t) = I0 sin(w t - p /2).
Okamžitá hodnota výkonu je
p(t) = i(t)u(t) = U0 sin(w t)I0 sin(w t - p /2) = U0 I0 sin(w t) (- cos(w t)) =
= - U0 I0 sin(w t)cos(w t) = - (1/2)U0 I0 sin(2w t).
Toto je harmonická funkce, její střední hodnota je nulová.
Na ideální cívce se elektrická energie nemění na teplo, ale na energii
magnetického pole. Energie jen periodicky kmitá mezi zdrojem a spotřebičem.
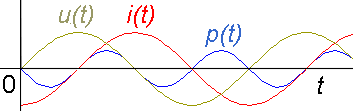
Reálná cívka má i elektrický odpor vinutí, proto je na ní nějaký reálný výkon a část energie se mění na teplo.
Na kondenzátoru "proud předbíhá napětí" o p/2,
jejich časové průběhy jsou u(t) = U0 sin(w t),
i(t) = I0 sin(w t + p /2).
Okamžitá hodnota výkonu je
p(t) = i(t)u(t) = U0 sin(w t)I0 sin(w t + p /2) = U0 I0 sin(w t)cos(w t) =
= (1/2)U0 I0 sin(2w t).
Toto je téměř tatáž funkce jako u cívky, její
střední hodnota je nulová. Na ideálním kondenzátoru se elektrická energie
nemění na teplo, ale na energii elektrického pole. Energie jen periodicky
kmitá mezi zdrojem a spotřebičem.
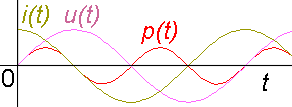
Reálný kondenzátor má nějaký konečný odpor, proto je na něm nějaký reálný výkon a část energie se mění na teplo.
V RLC obvodu se energie mění na teplo jen na rezistoru. Střední výkon je tedy dán jako P = RIef2. Vyjádříme efektivní hodnotu proudu pomocí amplitudy a tu pak pomocí amplitudy proudu a impedance obvodu.
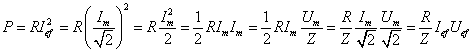
Výraz R/Z vyjádříme pomocí fázového posunu mezi proudem a napětím v obvodu. Z fázorového diagramu RLC obvodu ¤ plyne, že cosj = UR0 /U0 = RI0 /ZI0 = R/Z. Je tedy střední výkon P = UefIefcosj. Výraz cosj ... účiník. Čím je větší, tím větší je činný výkon v obvodu (tj. tím více energie se mění na teplo).
Chceme-li získat co největší výkon, musí být účiník co možná největší,
tj. výraz 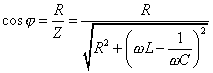 musí být co největší. A to bude tehdy, když člen
musí být co největší. A to bude tehdy, když člen ![]() bude nulový. Máme-li tedy například obvod s rezistorem a kondenzátorem, přidáním
cívky o vhodné indukčnosti se zvýší činný výkon v obvodu. Toto je
princip kompenzace účiníku.
bude nulový. Máme-li tedy například obvod s rezistorem a kondenzátorem, přidáním
cívky o vhodné indukčnosti se zvýší činný výkon v obvodu. Toto je
princip kompenzace účiníku.
Cívka navinutá na čtvercovém rámečku se stálou rychlostí w otáčí v homogenním magnetickém poli. Maximální napětí, které se indukuje v cívce, je 10 V. Určete napětí indukované v cívce o okamžiku, kdy normálový vektor k ploše cívky svírá se směrem indukčních čar magnetického pole úhel a) 0, b)p/4, c)p/2. Dále vyjádřete závislost napětí indukovaného na cívce na čase.
| Um = 10 V a1 = 0 a2 = p/4 a3 = p/2 u(t) = ? |
Předpokládejme, že v čase 0 je plocha cívky
kolmá na směr indukčních čar, tj. normálový vektor je rovnoběžný
se směrem indukčních čar. Jelikož se cívka otáčí stálou úhlovou
rychlostí w, mění se průmět
plochy cívky do směru indukčních čar jako Ssin(w t)
(w t je úhel, který svírá
normálový vektor k ploše se směrem magnetické indukce). Tedy časový
průběh napětí indukovaného na cívce je u(t) = Umsin(w t).
a) w t = 0
... u(t) = Umsin0= 0
|
Rezistor o odporu 100 W je připojen ke
zdroji střídavého napětí. Časový průběh napětí je na obr. 21. Určete
a) amplitudu, periodu a frekvenci napětí,
b) vztah pro okamžitou hodnotu napětí v závislosti na čase,
c) amplitudu, periodu a frekvenci proudu v obvodu,
d) vztah pro okamžitou hodnotu proudu v závislosti na čase,
e) časový diagram střídavého proudu,
f) fázový rozdíl mezi proudem a napětím v obvodu.
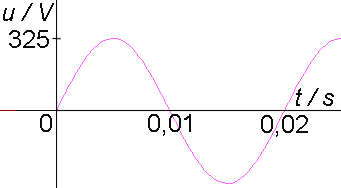
obr. 21
| R = 100 W | a) Amplituda napětí je jeho maximální
hodnota, tedy Um = 325 V; perioda je nejmenší čas, za který se časový průběh začne opakovat, tedy T = 0,02 s; mezi periodou a frekvencí platí vztah f = 1/T = 50 Hz. b) Napětí má harmonický sinusový průběh, tedy u(t) = Umsin(w t) = Umsin(2p ft) = 325sin(100p t) V. c) Jde o obvod s rezistorem, tedy mezi napětím a proudem platí Ohmův
zákon i(t) = u(t)/R, tedy Im = Um/R = 325/100 A = 3,25 A; d) Proud má harmonický sinusový průběh, tedy i(t) = Imsin(w t) = Imsin(2p ft) = 3,25sin(100p t) A. e) f) Napětí i proud dosahují maxim a minim ve stejných okamžicích, fázový rozdíl mezi nimi je nulový. |
V obvodu na obr. 22 je amplituda napětí na rezistoru 100 V a amplituda proudu 2 A. Jaké údaje ukazuje voltmetr a ampérmetr? Jaký je odpor rezistoru?
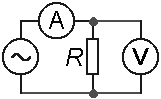
obr. 22
| Um = 100 V Im = 2 A U = ? I = ? R = ? |
Ve střídavém obvodu ukazují ampérmetry
a voltmetry efektivní hodnoty proudu a napětí. Údaj na voltmetru je
tedy |
Ideální cívka je připojena ke zdroji střídavého napětí o napětí 24 V a frekvenci 50 Hz. Prochází jí proud 0,05 A. Jaká je její indukčnost?
| U = 24 V I = 0,05 A f = 50 Hz L = ? |
Mezi napětím na cívce a proudem platí
vztah U = XLI = wLI = 2pfLI.
Z Toho je |
Na obr. 23 je RLC obvod napájený zdrojem střídavého napětí o frekvenci 50 Hz a efektivní hodnotě 115 V. Odpor rezistoru je 100 W, kapacita kondenzátoru 1 mF a indukčnost cívky 0,5 H. Jaký proud prochází obvodem? Jaký je fázový rozdíl mezi napětím a proudem? Jaký je činný výkon v obvodu?

obr. 23
| U = 115 V f = 50 Hz R = 100 W C = 1 mF = 1.10-6 F L = 0,5 H I = ? j = ? P = ? |
Celková impedance obvodu je 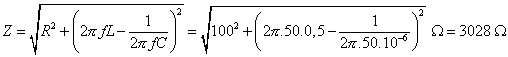 Proud procházející obvodem je Proud je ve fázi s napětím na rezistoru, fázový rozdíl mezi celkovým napětím a proudem je tedy stejný jako fázový rozdíl mezi celkovým napětím a napětím na rezistoru. Z fázorového
diagramu ¤ je vidět, že cosj = UR0 /U0 = RI0 /ZI0 = R/Z = 100/3028 = 0,033,
tedy j = 88,1º. Abychom
zjistili, zda napětí předbíhá proud nebo naopak, zjistíme, zda je
větší induktance cívky XL nebo kapacitance kondenzátoru
XC. Výkon v obvodu je P = UefIefcosj =115.0,038.0,033 W = 0,14 W. |
DOMÁCÍ ÚKOL:
1. Sériová kombinace rezistoru s odporem R, cívky s indukčností L a kondenzátoru s kapacitou C je připojena ke zdroji střídavého napětí. Na rezistoru je napětí o efektivní hodnotě 10 V, na kondenzátoru 8 V a na cívce 13 V. Určete efektivní hodnotu výsledného napětí na všech prvcích dohromady s použitím fázorového diagramu.
2. V obvodu stejnosměrného proudu, kde napětí zdroje je 25 V, prochází cívkou proud 0,05 A. V obvodu střídavého proudu se zdrojem o napětí 60 V a frekvencí 500 Hz jí prochází proud 0,0025 A. Vypočtěte odpor, impedanci, induktanci a indukčnost cívky a fázový posun mezi napětím a proudem v obvodu.
3. K elektrické síti o napětí 230 Hz a frekvenci 50 Hz je připojena cívka o indukčnosti 0,2 H a odporu 25 Hz. Jak velké je teplo, které předá cívka do okolí za jednu minutu?
62. hodina - čtvrtek 27.5. 2004
Test na zesilovač - zadání zde ¤.