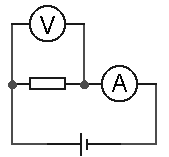
 schéma 1 |
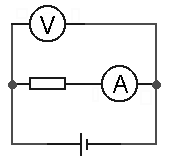 schéma 2 |
Zápisy do sešitu: El. náboj a síla Elektrické pole Práce v el. poli Rozložení náboje na vodiči Vodič v el. poli Izolant v el. poli Kapacita, kondenzátor El. proud Vodiče, polovodiče, nevodiče Prakt. práce: měření VA char. rezistoru Ohmův zákon Rezistor, reostat, potenciometr Spojování rezistorů Ohmův zákon pro celý obvod Kirchhoffovy zákony Vlastní polovodič Termistor Fotorezistor Dioda - pokusy Příměsový polovodič Princip diody Usměrňování diodou Graetzovo zapojení Praktické ovládání generátoru a osciloskopu Náhr. schéma diody Kondenzátor ve střídavém obvodu Kapacita diody VA char. diody a Zenerovy diody Zdvojovač napětí Televize a osciloskop Urychlování elektronů Vychylovací destičky Stacionární magnetické pole Magnetická síla (zač. a pokr.) Magn. poli přímého vodiče Mag. pole závitu a cívky Nabitá částice v mag. poli Shrnutí televize a osciloskopu Síla působící mezi dvěma vodiči Stejnosměrný elektromotor Magnetické vlastnosti materiálů Elektromagnet El. zvonek Elmag. relé Druhy elektromotorů Elmag. indukce - vznik ind. napětí Faradayův zák. elmag. ind. Magn. ind. tok Ind. proud Vířivé proudy Vl. indukce Zhášecí obvody cívek Rekuperační dioda Energie el. a mag. pole El. proud v plynech Jiskrový výboj Obloukový výboj Doutnavý výboj Koróna, katodové a kanálové záření LED Žárovka Bipolární tranzistor Unipolární tranzistor Operační zesilovač Práce a výkon Ef. hodnota proudu Regulace výkonu Tyristor Přenos rádiového signálu Amplitudová modulace Frekvenční modulace Sériový RLC obvod Fázorový diagram Elmag. oscilátor Výkon v RLC obvodu Amplitudová demodulace (krystalka) Frekvenční demodulace Rádiový přijímač Stereofonní vysílání Televize El. proud v kapalinách
12. hodina - pondělí 20.10. 2003
Vzor protokolu:
Pomůcky: zdroj napětí (akumulátor), ampérmetr, voltmetr, rezistor na destičce, spojovací vodiče
Postup: Obvod zapojíme dle schématu 1 nebo 2. Napětí měníme tak, že postupně zapojujeme různý počet akumulátorových článků. Měříme napětí na rezistoru a proud jím procházející.
 schéma 1 |
 schéma 2 |
Výsledky:
Tabulka:
| U/V | ... | ... | ... | ... | ... |
| I/mA | ... | ... | ... | ... | ... |
Graf:
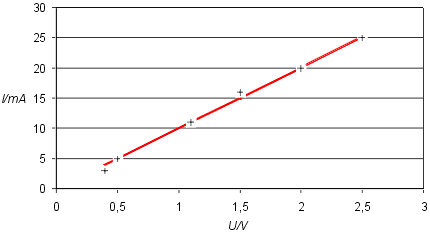
Diskuze: Naměřená VA charakteristika rezistoru je přibližně lineární. Chyby mohly být způsobeny chybami při odečítání ze stupnice a chybami měřidel.
Závěr: Pracovní úkol jsme splnili, změřili jsme VA charakteristiku rezistoru.
13. hodina - čtvrtek 23.10.2003
Minule jsme prakticky měřili závislost proudu procházejícího vodičem na napětí na vodiči. Zjistili jsme, že tato závislost je lineární.
Ohmův zákon: Proud I procházející vodičem je přímo úměrný napětí U na vodiči.
U = RI
R ....... konstanta úměrnosti - elektrický odpor vodiče, jednotka ohm W
el. odpor vodiče závisí na:
délce vodiče l (čím větší délka, tím větší odpor)
průřezu vodiče S (čím větší průřez, tím menší odpor)
materiálu vodiče ..... měrný elektrický odpor r, jednotka Wm (ohmmetr)
![]()
Měrný el. odpor závisí na teplotě - ![]()
a ......teplotní součinitel odporu
(Při vyšší teplotě se elektrony více sráží s atomy mříže, poněvadž
ty více kmitají.)
Vedení proudu ve vodiči - elektrony konají chaotický pohyb rychlostí zhruba 105 -106 m/s. Při připojení na zdroj el. napětí na ně začne působit el. síla, takže konají i posuvný pohyb rychlostí řádově 10-3 m/s.
Měření odporu - ohmmetr.
Úloha: Při jaké teplotě má měděný drát
1,1 krát větší odpor než při teplotě 20°C? Měrný elektrický odpor mědi
při teplotě 20°C r = 1,7.10-8 Wm,
teplotní součinitel odporu a = 4,0.10-3 K-1.
Řešení: Je ![]() , po
dosazení 1,1r0 = r0(1 + 4,0.10-3Dt)
, po
dosazení 1,1r0 = r0(1 + 4,0.10-3Dt)
Dt = 25°C, tedy t = 45°C.
Hledaný odpor bude drát mít při teplotě 45°C.
Při ochlazování některých kovů dochází při teplotě blízké O K k úplnému vymizení el. odporu - supravodivost.
DOMÁCÍ ÚKOL:
1. Kolikrát se zvýší el. odpor vlákna rozsvícené žárovky oproti zhasnuté?
2. Vymyslete princip ohmmetru.
14. hodina - čtvrtek 30.10. 2003
vodivost G ....... ![]() .
Jednotka siemens S
.
Jednotka siemens S
15. hodina - pondělí 3.11. 2003
Rezistor - 2 zdířky, konstantní odpor
Reostat - dvě zdířky, jedna pevná, druhá spojena s
jezdcem (barevně označena)
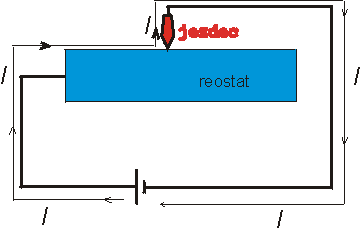
Proud protéká jen částí reostatu - změnou polohy jezdce se mění odpor
reostatu (když jde jezdec doleva, odpor reostatu klesá).
Potenciometr - zapojeny všechny tři zdířky
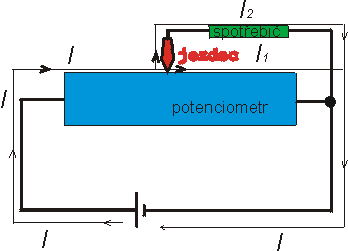
Proud protéká celým potenciometrem, na jezdci se dělí a část ho teče také
spotřebičem.
Spojování rezistorů - sériově a paralelně
Sériové zapojení
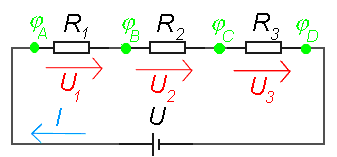
obr. 5: Sériové zapojení rezistorů
Všemi rezistory protéká stejný proud I. Součet napětí
na rezistorech je roven napětí zdroje - U = U1 + U2 + U3.
Dosadíme z Ohmova zákona ... ![]() a vykrátíme proud I.
a vykrátíme proud I.
![]()
Paralelní zapojení
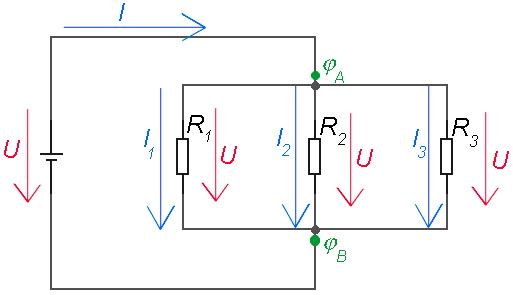
obr. 7: Paralelní zapojení rezistorů
Na všech rezistorech je stejné napětí a součet proudů jimi protékajících
je roven celkovému proudu protékajícímu zdrojem I = I1 + I2 + I3.
Dosadíme z Ohmova zákona ..... ![]() a vykrátíme napětí.
a vykrátíme napětí.
![]()
16. hodina - čtvrtek 6.11. 2003
Potenciometr - jaký proud protéká jednotlivými částmi a zátěží?
Rozdělíme potenciometr v místě jezdce na dva rezistory R1 a R2.
Zátěž je označena R.
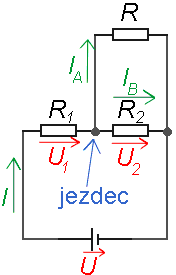
Proud I se na jezdci dělí na proudy I1 a
I2, tedy platí I = I1 + I2.
Dále je U = U1 + U2.
Napřed je třeba vypočítat proud I. K tomu je nutné napřed určit
celkový odpor v obvodu pomocí pravidel o spojování rezistorů. Předpokládáme,
že odpory všech rezistorů jsou známé a dále je známé napětí zdroje.
1. Paralelní kombinaci rezistorů R a R2 nahradíme
rezistorem Rekv. Ten má odpor Rekv; ![]()
2. Sériové spojení rezistorů R1 a Rekv
nahradíme rezistorem Rc. Ten má odpor ![]()
3. Vypočteme celkový proud obvodem I: 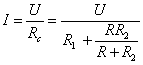
4. Vypočteme napětí U1: 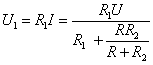
5. Vypočteme napětí U2 (to je napětí na
rezistoru R i R2): 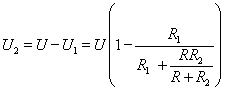
6. Vypočteme proud IA: 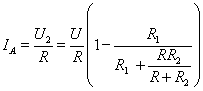
7. Vypočteme proud IB: 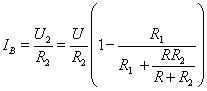
To, co je pro nás zajímavé, je napětí na zátěži (rezistor R) a proud jí procházející.
DOMÁCÍ ÚKOL: Zamyslet se, jak se tento proud a napětí mění s pohybem jezdce doleva (tj. klesá R1 a zvětšuje se R2) a doprava (tj. klesá R2 a zvětšuje se R1).
Ohmův zákon platí pro kovový vodič. Jak je tomu s baterií. Je napětí baterie, kterou neprochází proud, stejné, jako když jí proud prochází?
Pokus: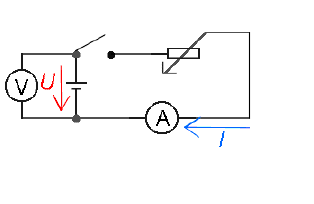
Když je spínač rozpojen, ukazuje voltmetr jistou hodnotu napětí (elektromotorické
napětí Ue).
Sepneme spínač a zmenšujeme odpor reostatu. Proud obvodem roste. Zapíšemeněkolik odpovídajících si hodnot proudu obvodem a napětí na zdroji.
| proud I/A | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| napětí U/V | 20 | 18 | 17 | 14 | 12 | 9 | 8 | 6 | 5 | 2 | 0 |
Závěr: Zvětšuje-li se proud protékající obvodem, klesá napětí mezi svorkami zdroje napětí (tzv. svorkové napětí zdroje U)
Zdroj napětí má elektrický odpor (tzv. vnitřní
odpor zdroje Ri). Zdroj pak kreslíme jako sériovou kombinace ideálního zdroje napětí
(nemá vnitřní odpor, jeho napětí je rovno Ue) a rezistoru
s odporem rovným vnitřního odporu zdroje.
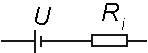
| Obvod s reálným zdrojem napětí a rezistorem
o odporu R. Celkový odpor v obvodu je R+Ri (sériové
zapojení) a tedy proud protékající obvodem je
Toto je jedno z vyjádření Ohmova zákona pro celý obvod. Vztah můžeme přepsat Součin RI je roven napětí na rezistoru, které je zároveň rovno napětí zdroje (tj. svorkové napětí U, které měří voltmetr). Tedy máme
Je vidět, že čím větší proud I prochází obvodem, tím je svorkové napětí U nižší. Proud může dosáhnout až takové hodnoty, že svorkové napětí bude nulové. Tehdy se nazývá zkratový proud. Jeho velikost je Iz = Ue/Ri. |
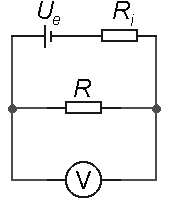 obr. 4 |
DOMÁCÍ ÚKOL: Vypočtěte vnitřní odpor, elektromotorické napětí a zkratový proud zdroje napětí, jehož VA charakteristika je nahoře.
17. hodina - pondělí 10.11. 2003
Pro výpočet proudů tekoucích obvodem.
Názvosloví:
UZEL - místo v obvodu, kde se vodivě stýkají nejméně tři vodiče (na příkladu
to jsou body A a B)
VĚTEV - část obvodu mezi dvěma uzly - všemi prvky v jedné větvi protéká
stejný proud (na příkladu to jsou všechny úseky mezi
body A, B)
1. Kirchhoffův zákon: Součet všech proudů přitékajících do uzlu je v každém okamžiku roven nule. Proudy tekoucí do uzlu bereme se záporným znaménkem a proudy vytékající z uzlu s kladným znaménkem.
Zapsáno rovnicí: I1+I2+I3+...=0
2. Kirchhoffův zákon: Součet napětí na všech prvcích (aktivních (zdrojů) i pasivních (rezistorů,...)) podél uzavřené smyčky je v každém okamžiku roven nule. Přitom napětí na rezistorech vyjadřujeme jako U=RI, kde R je odpor rezistoru a I proud jím protékající. Je-li smyčka orientována souhlasně se šipkou značící směr proudu nebo polaritu zdroje (zde šipka směřuje od + pólu k - pólu), bereme příslušný člen s kladným znaménkem, v opačném případě se záporným znaménkem.
Zapsáno rovnicí U1+U2+U3+...=0
Volba směru šipek na začátku je libovolná, potom se však už musí dodržovat.
Máme elektrický obvod se dvěma bateriemi a třemi rezistory (obr. 1). Vypočtěte proudy tekoucí jednotlivými větvemi a napětí na jednotlivých rezistorech.
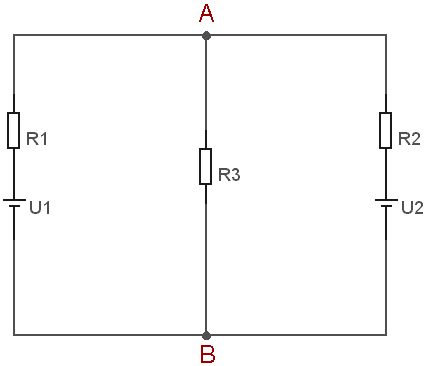 |
Hodnoty odporů a napětí:
U1=10 V R1=10 W |
1. Označíme si v obrázku šipky u zdrojů napětí (od "+ k -") a vyznačíme libovolně směry proudu v jednotlivých větvích. Dále si zvolíme uzavřené smyčky (stačí jich tolik, kolik "okének" je ve schématu, v tomto případě tedy dvě).
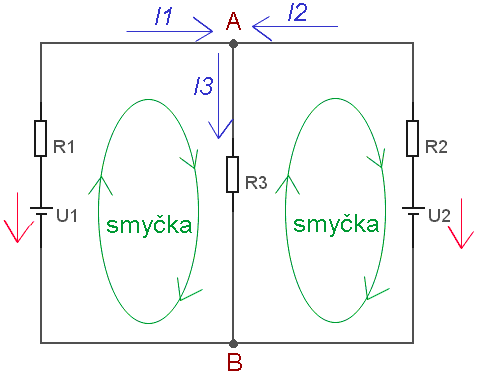 |
Smyčka vlevo má stejnou orientaci jako proudy procházející
rezistory R1a R3 a opačnou než napětí
zdroje U1.
Smyčka vpravo má opačnou orientaci než proudy procházející rezistory R2a R3 a stejnou jako napětí zdroje U2. |
2. Napíšeme první Kirchhoffův zákon např. pro uzel A: Proudy I1 a I2 vtékají do uzlu (tedy kladné znaménko), proud I3 z uzlu vytéká (tedy záporné znaménko).
I1+I2 - I3 = 0 (neboli I1+I2 = I3)
3. Napíšeme druhý Kirchhoffův zákon pro obě smyčky:
levá smyčka: R1I1+R3I3 - U1 = 0
pravá smyčka: -R2I2 - R3I3 + U2 = 0
4. Máme teď tři rovnice pro tři proudy I1, I2, I3:
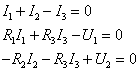
Tyto rovnice vyřešíme. Jelikož obecné řešení je komplikované, zavedeme místo I1, I2, I3 proměnné i1, i2, i3 označující číselné hodnoty proudů (v ampérech) a za odpory a napětí dosadíme jejich číselné hodnoty (v základních jednotkách, tj. ohmech, resp. voltech).
Máme rovnice 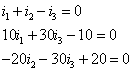
Ty vyřešíme. Výsledkem jsou čísla i1 = -1/11,
i2 = 5/11, i3 = 4/11, tedy
proudy
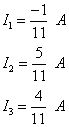
Proud I1 vyšel se záporným znaménkem. Znamená to, že jeho skutečný směr je opačný než směr námi zvolený. U ostatních proudů souhlasí zvolené směry se skutečnými.
Napětí na jednotlivých rezistorech se spočte z Ohmova zákona.
Další úlohy jsou ve sbírce příkladů, kapitola 1 ¤ nebo můžete zkusit tyto aplety:
| Kirchhoffovy zákony - obvod 1 ¤ | Kirchhoffovy zákony - obvod 2 ¤ | Kirchhoffovy zákony - obvod 3 ¤ |
| Kirchhoffovy zákony - obvod 4 ¤ | Kirchhoffovy zákony - obvod 5 ¤ |
DOMÁCÍ ÚKOL: Spočtěte vztahy pro dělící poměr děliče napětí a
proudu.
Dělič napětí: 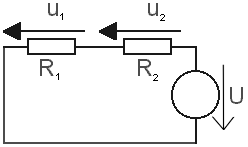
Znáte odpory rezistorů a napětí U
zdroje. Vypočtěte napětí u2.
Dělič proudu: 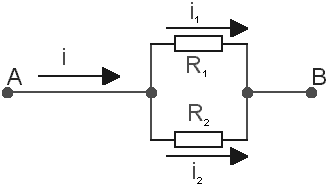
Znáte odpory rezistorů a proud
i. Vypočtěte proud i1..
Na řešení se můžete podívat zde.